The story of quantum mechanics is a very weird one. Because that is how the quantum world is, totally counter-intuitive, absurd, and nonsensical. The reason why it is so is that our brains are adapted to understand the world as we can see it, and whatever we see is only the classical approximation. Humans tend to search for logic in a statement based on their experiences. The quantum mechanical absurdity seems unreasonable because there is no way we can experience these in our classical perception. Spin too is one of such phenomena we stumble in understanding.
The Story of Spin
In the initial formulations of quantum physics, things were relatively easy. You wanted to explain an electron, just take the mass and charge and you had the complete description of it. Nothing else was required to explain an electron. But unfortunately to the physicists, the tables got turned when Stern-Gerlach performed their silver atom experiment.
What they did was heat some silver atoms in an oven, and collimate the silver atoms from the oven forming a single beam and then pass it through a magnetic field, say in the z-direction.
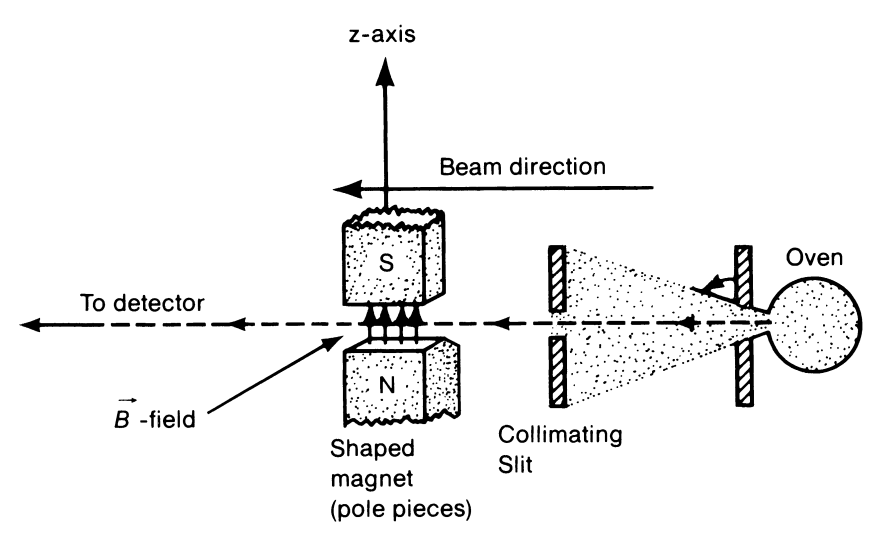
To oversimplify the model, the silver atom is entirely neutral, and it has a magnetic moment which depends only on the outermost electron.
Since the orientation of all the atoms is random, the expected outcome is a spread along the z-axis with a gaussian distribution. This is what anyone with their right minds would expect.
But the result totally revolutionised the world of physics. The beam had split exactly into two parts. About half of the atoms had gone upwards and the other half downwards.

(Image: docplayer.net)
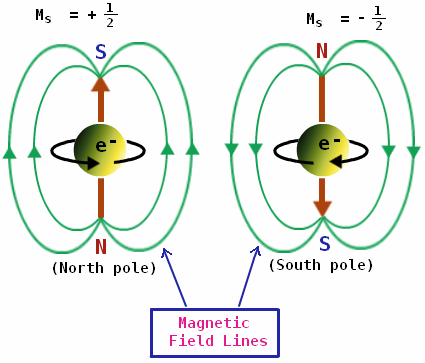
This could only mean that the electron had an angular momentum of its own causing a magnetic moment. This angular momentum was discrete, i.e only in two possible directions, either upwards or downwards, and nothing in between. Since this angular momentum was as if the electron was spinning independently about an axis of its own, it was called the spin. This spin can indeed exist in any possible direction, but upon measured, we get only one of the two possible directions.
By then another physicist, sir Wolfgang Pauli, while trying to explain the structure of an atom and the states of the electron, gave his exclusion principle and also stated that the two electrons possible in a given orbital had opposite spins thus making them non-identical and hence allowing the exclusion principle to be satisfied.
Click here to read more about the exclusion principle.
What is it and Where does it come from?
Spin is the property of all particles just like mass and charge are. Angular momentum is a conserved quantity, and so is spin. Also, the total angular momentum for a system is not conserved unless we count in the spin. This is the reason spin is associated with the intrinsic angular momentum of particles. It is also responsible for the magnetic moment of these particles.
(Image: Byju’s)
The mathematical description of quantum mechanics in the early stages had no signs of spin. This is because initially, it was as if it had no reason to exist mathematically. It was something that was introduced only to explain the phenomenon like the Stern-Gerlach experiment, or the states of electrons in an atom and so on.
But when P.A.M Dirac amalgamated relativity with quantum physics, it was soon noticed that spin was an essential requirement of the relativistic quantum theory. It arises from the rotational symmetry of nature.
Spin and Symmetry
As stated above, the spin arises out of the rotational symmetry of fields in nature.
Consider a scalar field, where every point in space is associated with a scalar quantity, or to put simply, with a number. If you take the field at any point and rotate it by any angle, the number at that point does not change. This scalar field is called spin-zero field. The Higgs field is an example of the spin-zero field.
The vector field has every point in space associated with a vector. Now if you take a vector at some point and rotate the coordinate system, the components of the vector do change. But a rotation by 360° brings back the original vector. Thus the vector field is invariant under rotation by 360°. This vector field is called a spin-one field. The electromagnetic field is an example of the spin-one field.
There are fields in nature which are invariant under rotation by 180°. These are called tensor fields, with each point in space associated with a tensor. These tensor fields are called spin-two fields. The gravitational field is a tensor field and hence is a spin-two field.
From QFT, every particle has an associated field and vice versa. So the particle corresponding to the scalar field will have zero spin, the one corresponding to vector field will have spin one, and the one corresponding to the tensor field will have spin two.
Thus the Higgs Boson is a spin-zero particle, photons spin-one, and gravitons spin-two.
What we can notice here is that spin-one field is invariant under rotation by 360°, spin two is invariant under 180°, and so on. So from the same pattern, it is obvious that a spin “n” field would be invariant under rotation by (360/n)°. Thus a spin ½ field should be invariant under rotation by 720°. Such a field is called a spinor field, with every point in space associated with a spinor. A spinor is a “weird” type of vector, which upon rotation by 360°, gets reversed. The electron field is a spinor field, invariant under 720° rotation. Thus the corresponding electron has spin one half.

Notice that upon single rotation of the cube, the whole system is inverted. The system gets back to its original state only upon completion of two rotations.
[GIF: gyfcat}
The Physical Meaning of Spin
Most people believe that the electron is actually spinning about some axis to generate the spin angular momentum.
This is entirely wrong because the electron is considered a point particle, and for a point particle to generate a finite angular momentum, it should be spinning infinitely fast.
If you argue saying that electron is a wave packet with some finite size, say the Compton wavelength, then too, the electron’s surface must be spinning at a velocity greater than that of light. So the intuitive of an electron spinning is a wrong one and should be discarded.
But what about fields, fields can have angular momentum. And any particle is an excitation of its underlying field. So a possibility is that the spin of particles as we see it could be, in fact, the angular momentum of the corresponding field. The angular momentum carried by the electron field could be present to us as the spin of the electron and so on.
But all of this is still only a hypothesis. No concrete idea is present for the physical meaning of spin. That is why it is not a wonder that it is one of the most confusing aspects of quantum mechanics.
To conclude, it is best to quote Feynman,
” I think I can safely say that nobody understands quantum mechanics.
If you think you understand quantum mechanics, you don’t understand quantum mechanics.”




many thanks for offering me such info, it is really
insightful.
[…] Generally, qubits are made of same semiconducting material as usual electronics materials. But now for the first time chemists and physicists at Northwestern University and University of Chicago have developed a new method to create tailor-made qubits. This was done by chemically synthesizing molecules that encode quantum information into their magnetic or ‘spin’ states. […]
Spin is indeed a confusing subject just like Turbulence.
Does wave mechanics take into consideration the spin of electron? And if spin is the property of field then why not all fermions have same spin?
Wave mechanics, I believe, depends entirely on the Schrodinger wave equation to formulate the equations for atoms and subatomic particles. Since Schrodinger equation DOES NOT consider the spin aspect, wave mechanics does not entirely take into account the spin.
Fields cannot carry angular momentum in all values. Only specific values of angular momentum is allowed for a given field, and this is different for different fields. Since “DIFFERENT FERMIONS ARE EXCITATION OF DIFFERENT FIELDS – ELECTRON, OF ELECTRON FIELD; QUARK, OF QUARK FIELD, ETC”, and these different fields carry different amount of angular momentum, so spin is different for different fermions.