The 2nd law of thermodynamics can be stated in many ways and all of them are correct. The most common form of the second law of thermodynamics states that the entropy of a system always increases with time, i.e. . This law is so important in physics that if you pen a theory that violates conservation of energy or charge, it’s fine, but it should not violate the 2nd law of thermodynamics.
In the 21st century, this law seems to be simple and straightforward, but the scenario was not like this in the 19th century. There have been many objections regarding this law, and there still are many. Some of them are so important, and let us go through them today.
Loschmidt’s reversibility objection.
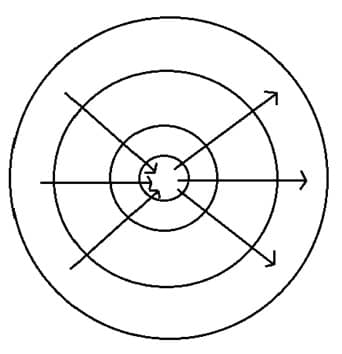
The basic underlying principle of statistical physics is Newton’s laws. The particles described in Maxwell-Boltzmann statistics obey Newton’s laws. The Newton’s laws have a property that they obey time symmetry, i.e. for every possible motion forward in time there is also another possible motion that happens backwards in time, just with the reversed direction of momentum.
Loschmidt objected by stating that, from the symmetry property of Newton’s laws, for every arrow in phase space with , there is an arrow with
. And his objection was indeed correct.
The solution for this objection is as follows:
We need to break the symmetry and that can be done by introducing a boundary condition. The particular boundary condition we impose is called the past hypothesis.
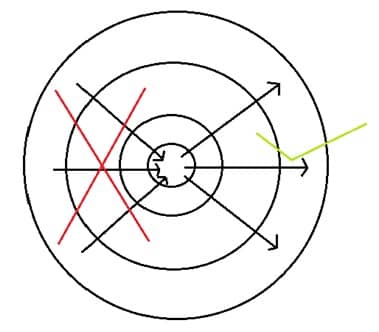
Past hypothesis: “Universe began in a low entropy state”. This causes all the arrows starting from high entropy state going towards low entropy state cancels. This thing is indeed true, as near the big bang, the universe started with a very low entropy. But we really don’t have any idea why the early had very low entropy. That is the question that is unanswered yet.
Zermelo’s Recurrence Object:
Henri Poincaré once stated that “a closed bound classical system returns to any configuration infinitely often”.
What this means is that supposed we have a configuration of some particles and we let the system evolve, then Poincaré says that if we wait long enough, the system will come back to its initial state once in a while and the process repeats itself.
Ernst Zermelo was a mathematician and he made an objection using Poincaré’s statement. He said, “a function S(t) (entropy as a function of time) can’t be both recurrent and monotonic.” I.e. we can’t have the same entropy state as initial if the entropy is increasing in any one direction.
Ludwig Boltzmann tried to give a solution to this by the means of what we call today the “Anthropic principle.” Notice that all this happened in the 19th century, when there was no General relativity, and hence we lived in a Newtonian world. He said that, for all the matter in the universe we have a certain maximum value of entropy, what we call Smax. We know that if the system is in a certain entropy state, and is not increasing, then life is not possible. So system can’t possibly be in the maximum entropy state.
But there can be fluctuations, some small and some big. The fluctuations can repeat in time, so there is the recurrence Zermelo was talking about. Boltzmann stated that when there is a large fluctuation, i.e entropy goes down and then starts increasing again, this is the time when planets and galaxies and stars are formed. We are in such a fluctuation right now.
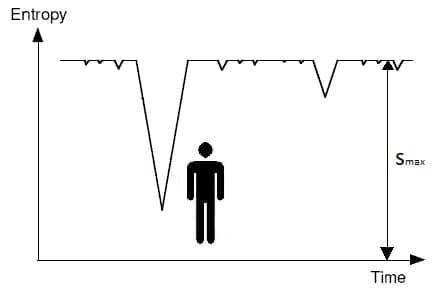
But there is a problem to this theory, referred to as “Boltzmann Brains”. We can’t live in such a fluctuation because such fluctuations are very rare. Say sometimes there is a small fluctuation and only the brain is formed, and with another fluctuation, only the body is formed. But to form a complete body, all these fluctuations have to happen at the same time which is extremely rare.
One more problem to this is, if it were to happen that all the fluctuations are non-interacting, we cannot sense any other human being or anything. But this is not the case, we can in fact sense things and human beings, so something is wrong with this theory and thus cannot be accepted.
There had been better solutions to come across but none of them had been so satisfactory. The 2nd law has been very important, and at the same time very confusing for us. Maybe someday, we will have a complete theory explaining all of this.