Riemann Hypothesis: The Prime Obsession of Mathematicians

hypothesis

Mathematics aficionados always concede mathematics as supreme beauty with unanticipated links in natural sciences. This beauty is ineffable. One can find it with sense of aesthetics and abstraction. However it’s really tough for non experts to find beauty in prodigious complex equations. According to Occam’s Razor (Principle of Parsimony) entities should not be multiplied without necessity.

There are many mathematical results whose formulations can be understood by non-mathematicians, and whose beauty can surely be understood by many. Simplest explanation is usually the right one. Prime numbers are the very atoms in number theory. Prime numbers have always fascinated mathematicians. They materialize among the integers seemingly at random, so far not discrete they appear to be some order or pattern. Composite numbers wear prime numbers on their sleeve.

Infinitude of Prime numbers:

hypothesis

Euclid (300 BCE) was soon to prove there are infinitely many primes by method of Contradiction. His proof is the classic example of reductio and absurdum. This is a method of logic whereby one assumes a statement is false and shows this leads to ‘absurdity’. But mathematicians assumes there are only finitely many primes. They seek to glean an ‘absurdity’ from this assumption. Let’s presume there are one million primes, but no more. Multiply all of these one million primes together and then add one to the answer. Call this huge number N.

Now what is the remainder when you divide N by one of the primes? Answer is One!! This means that N is not divisible by any prime! This is our ‘absurdity’.

Euclid’s theorem tells us that there are infinitely many primes, but doesn’t give us a good recipe for finding them all. The largest explicitly known prime is  

                                                     2^32,582,657– 1

Which is 9,808,358 digits long and was shown to be prime in 2006 by the GIMPS distributed internet project.

In spite of not having an exact  formula for the sequence of primes, we do have a fairly good inexact formula.

Riemann Complex Conjecture:

hypothesis

The nineteenth-century mathematician Bernhard Riemann, who ascended the study of prime numbers in modern times more than anyone else, developed further tools needed to deal with it. Formal proof of theorem was given only in 1896 independently by Hadamard and de la Vallee- Poussin, after a century ago it had been stated. The Riemann hypothesis is a salient magnificent problem in number theory as its validity will aver the manner of the distribution of the prime numbers.

According to precepts of fractal geometry, phenomena which appears random when viewed, exhibit some orderliness and pattern which could be regarded as a fractal characteristic. For instance, the prime numbers are very arbitrary and haphazard entities, yet when viewed, they display a regularity in the way they thin out, whereby it is affirmed that the number of primes not exceeding a given natural number is approximately / , in the sense that the ratio of the number of such primes to / in due numbers approaches 1 as n becomes larger and larger, being the natural logarithm of . Limit of the quotient of the 2 functions

𝛑(n) ~ (n/ ln n )

Here is only a opportune symbol adopted to denote the prime counting function. This theorem called ‘The prime number theorem‘. This theorem states the frequency of prime numbers.  Frequency of number of primes around P in a given set is inversely proportional  to the number of digits in P. This result is one of the landmark achievements of number theory. The proof of this result uses much more advanced mathematics than Euclid’s proof, and is quite remarkable. 

Music of the Prime numbers:

hypothesis

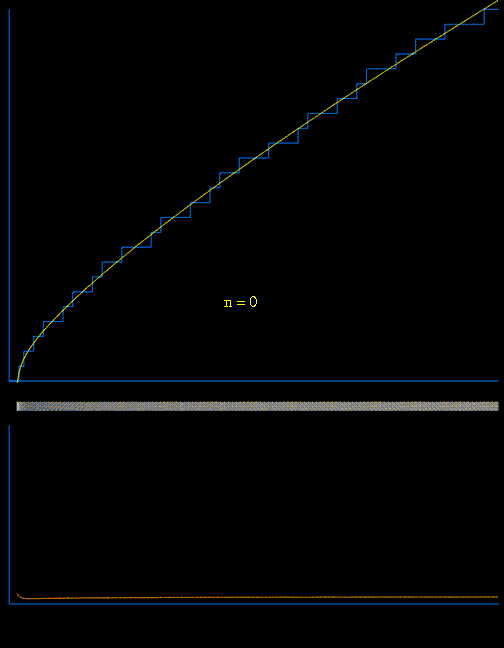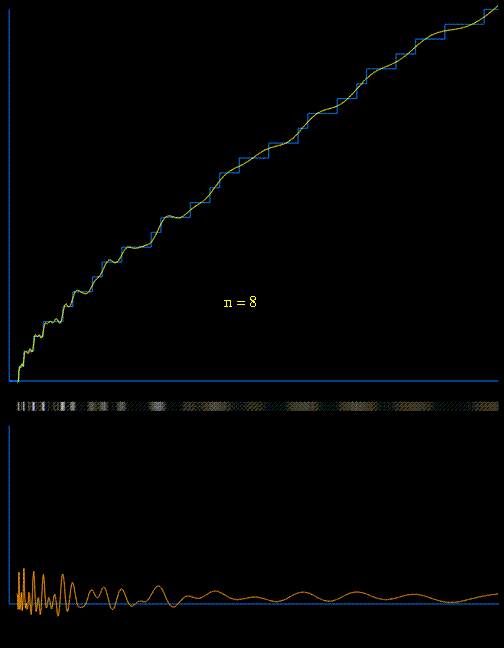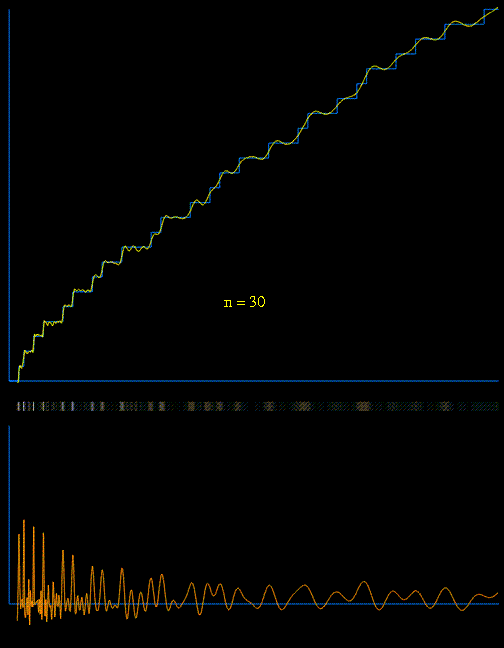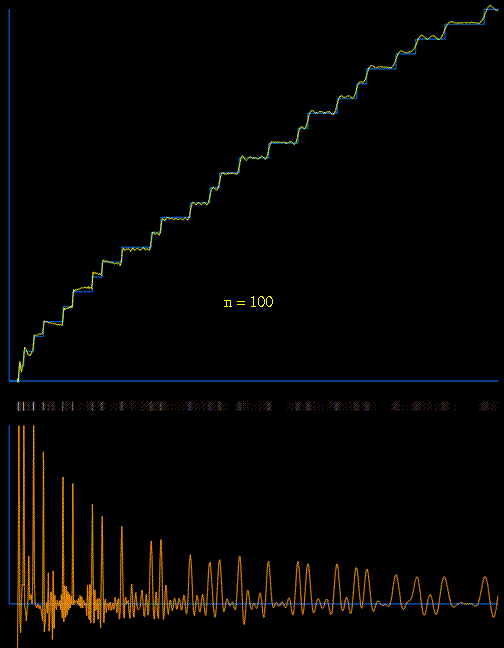
There is a very informal sketch of proof of this theorem. Create a ‘sound wave'(Von Mangoldt Function)which is noisy at prime number times, and quiet at other times.

.**.*.*…*.*…*.*…*…..*

‘Listen'(or take Fourier transforms) to this wave and record the notes that you hear(the zeroes of the Riemann zeta function or the ‘music of the primes’). Each such note corresponds to a hidden pattern in the distribution of the primes.

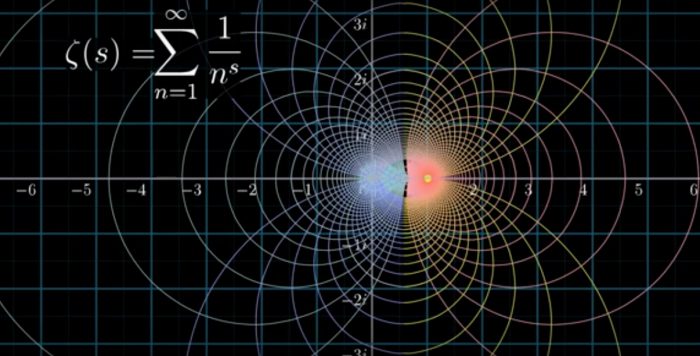
All this is despite the fact that the primes are meagre and meagre as n is larger and larger. The prime number theorem could be in fact be regarded as a weaker version of the Riemann hypothesis which put forward that all the non-trivial zeros of the zeta function ζ on the critical strip bounded by x=0 and x=1 would be at the critical line x=½.

It propounded that all the non-trivial zeros of the zeta function ζ lie on the critical strip between Re(x)= 0 and Re(x)=1 at the critical line Re (x) = ½. We define the Riemann zeta function as

   when |x|$\ge$ 1

At x= 1 this series is called the harmonic series and its sum is infinite. At x > 1,the series converges to a finite number as consecutive terms are added. If x < 1 then the sum is again infinite.

This zeta function is defined for all complex numbers except for x=1. The region  0$\le$Re(x)$\le$1 is called the critical strip. The zeros of the zeta function which lie outside the critical strip are called trivial zeros, would be found on an oscillatory sine-like wave which oscillates in spirals, there being an infinitude of these spirals (representing the so-called complex plane). A zero of a function is a point at which that function vanishes. A pole of a function f is a point at which, if 1/f is defined to be zero, then 1/f is homomorphic at Re(x)=1. Hadamard and de la Vallee Poussin had in 1896 independently proven that none of the non-trivial zeros lie on the very edge of the critical strip, on the lines Re(x)=0 or Re(x)=1. One can deduce prime number theorem from this.

Riemann had posited that the margin of error in the estimate of the quantity of primes less than a given number with prime counting function 𝛑(x) is expressed in terms of the J(x) function which is a step function involving the non-trivial zeros expressed in terms of the ζ(x).

$J\left(x\right) = Li\left(x^{}\right) – \underset{p}{\sum Li\left(x^p\right) – }\log 2 + {\int }_x^{\infty }dt/\left\{t\right(t^2–1)\log t\}$

Where J(x)= exact quantity of primes less than a given number.

The zeta function has the property of prime sieving encoded within it, the properties of the prime counting function 𝛑(n) being somehow encoded in the properties of the zeta function. The characteristic of the primes on the input side of the function determines the characteristics of the zeros on the output side of the function zeros.

$\psi \left(x\right) = \sum _{pm\le x}\log p$

In this notation, p is a prime number and m is a positive integer. This function which imitates the distribution of the primes. It was created by Tchebychev. The distribution of primes determines the distribution of the zeros, so that from the study of the distribution of the zeros the distribution of the primes could be deducted and vice versa.

Even though the prime counting function 𝜋(n) of hypothesis provides a progressively better estimate of the quantity of primes towards infinity – there is no such really great disorder or irregularity among the primes, a state of affair which is plainly proclaimed by the fact that the corresponding non-trivial zeros at the critical line Re(x)= ½ on the critical strip between Re(x) =0 and Re(x)=1 display regularity in the way they line up at with no zeros appearing anywhere else on the critical strip.

However Riemann hypothesis has been found to be true for the 3×1012 non-trivial zeros. Non-trivial zeros at the critical line Re(x)=½ become more and more closely packed together the number line, the density of the one is approximately the reciprocal of the density of the other wherein the complementariness, regularity, symmetry is evident.  

The prime counting function 𝜋(n) provides a progressively better estimate of the quantity of primes towards infinity. If the non-trivial zeros of the zeta function of hypothesis lies outside critical strips then Riemann zeta would be of no use in those regions.

Recipe To Become Millionaire

hypothesis

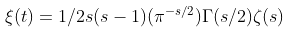
Zeta function has zeros at the negative even integers -2, -4, -6 and one refers to them as the trivial zeros. The other zeros are the complex numbers ½ + i 𝝰 where 𝜶 is a zero of ζ function. But non-trivial zero have real part ½.Now this is the conjecture and it’s one of the world’s seven ‘Millennium Prize Problems‘ divulged by Clay Mathematics Institute of Cambridge, Massachusetts for which it will pay a $ 1,000,000 prize for the solution! Hitherto if you’re not intrigued, maybe this prize will persuade you. This problem is superlative of all those problems.

hypothesis