We all know that the Quantum Computing Industry observed a boom in resources and funding over the last 2 decades. The largest of the Tech companies want to build a piece of this remarkable machinery and bag the title of “Quantum Supremacy.” The term itself is very hard to define, in other words, it is ineffable!
Now a quick recap: In the last article, I talked about the basics of quantum computing and the very basics of the RSA algorithm. I mentioned something about the Lightsaber if you can recall. Can’t recall here’s a link. (In case! 😜)

The Ultimate Quantum Computing Weapon
In the year 1980, then very famous Richard Feynman sir tried his hand at Quantum Computing. He proposed a very crazy idea that if we could somehow develop a machine that reads qubits, that would be the biggest miracle of mankind so far. The possibilities he could think of were endless. Besides doing tasks that supercomputers weren’t capable of doing (or took a long time 🥱), scientists at that time did not seem to have anything on the plate that would attract the attention of brilliant minds or heavy pockets.

The year 1994 changed the whole game when Peter Shor, an ex-Caltech sophomore published a paper that became the Crown Jewel of Quantum Computing syllabus. A paper that would set a roadmap for the future of Quantum Computing.
The Lightsaber: Shor’s Algorithm
The suspense is over now. As sketchy and techy as the name I gave it seems, this isn’t some kind of algorithm you can carry in your pocket, plug-in, and steal everything. It requires two major things, firstly a quantum computer and secondly error-reduction methods.

But let us first hear what Peter Shor has to say about his algorithm in his own words. “At first, I had only an intermediate result. I gave a talk about it at Bell Labs [in New Providence, New Jersey, where I was working at the time] on a Tuesday in April 1994. The news spread amazingly fast, and that weekend, computer scientist Umesh Vazirani called me. He said, “I hear you can factor on a quantum computer, tell me how it works.” At that point, I had not solved the factoring problem. I don’t know if you know the children’s game ‘telephone’, but somehow in five days, my result had turned into factoring as people were telling each other about it. And in those five days, I had solved factoring as well, so I could tell Umesh how to do it.”
In the previous article, I discussed the working basics of the RSA algorithm. All the encryption systems today use a composite number(N) that is a product of two co-prime numbers. The numbers are in the range of 200 digits. Shor’s algorithm provides an upper hand by providing a way to factor the number N and hence break the encryption.
Deciphering the Shor’s Algorithm
Now, this remarkable algorithm works in a certain number of steps. Any prior mathematical knowledge would prove beneficial now. (Just kidding! 😂)
Firstly, we have to choose a number ‘g’ (random) < N (composite number), a step that can be classically performed by human minds as well as traditional computers. One thing I’d like to mention is that ‘g’ doesn’t need to be an exact factor of N, but can also share factors with N.
Now I need you to understand one thing, that if A and B are co-prime then An = m*B + 1. (This is a proven formula.) Take 7 and 50, they don’t share a factor but 74 = 2401= 48*50 +1.
So our random guess follows gp = m*N +1 (p ≠ 0). Solving further gp -1 =m*N can be resolved into:
(gp/2 + 1)*( gp/2 – 1)= m*N
The terms on the left-hand side are the new and improved guesses. No matter if the terms are multiples of the factors of N, we have a pretty darn 2000-year-old efficient algorithm called “Euclid’s algorithm.”
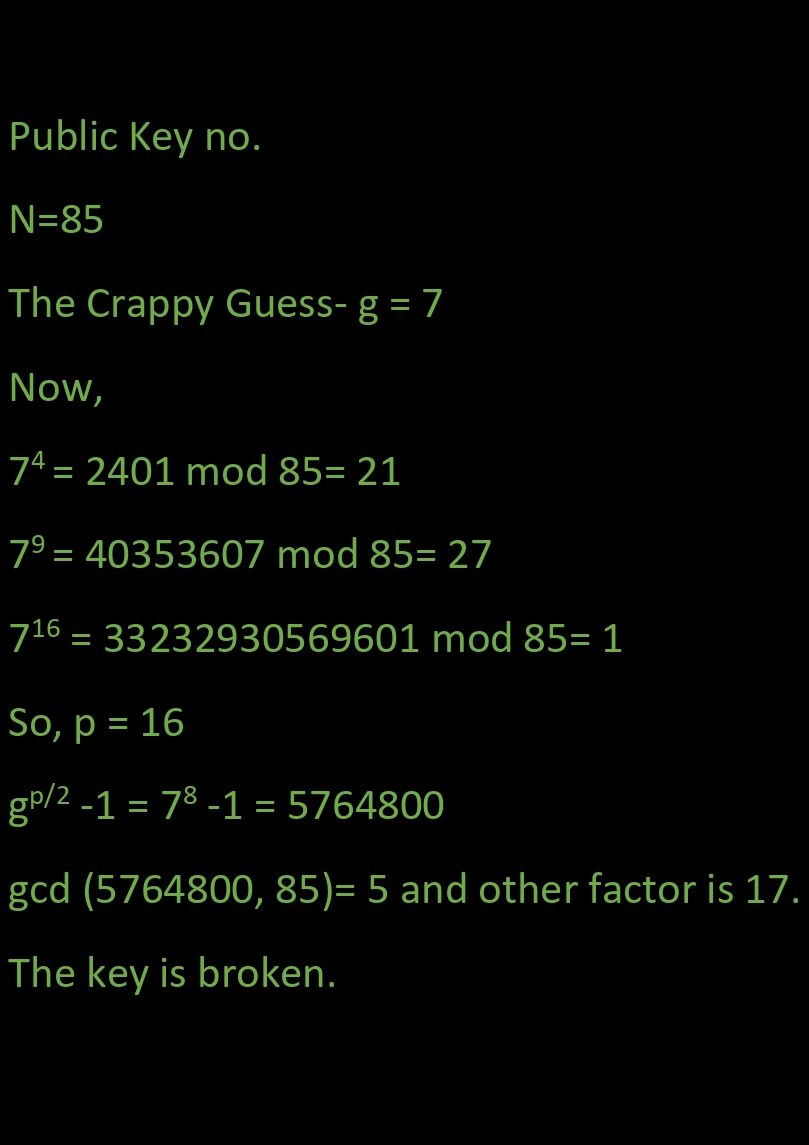
This is all folks, the algorithm that can break your privacy. But wait, you will say “If this is so simple, why can’t we run it on today’s computer already? 🤷♂️” I might say there are some major hurdles in between.
Traditional computers don’t have that much processing power to break the encryption. For reference, a normal desktop would take 2000 years to break a 78 digit long encryption. Secondly, there’s a slight chance that one of the numbers on the left side might be a multiple of N, in that case, the other would be a factor of ‘m’. Thirdly, the power ‘p’ might be odd, because of which we can’t use it.
But 37.5% of chance this algorithm works, great! But wait why is a Quantum Computer exactly needed? How do we find “p”? The answer lies in Quantum mechanics itself.
The Real Thief Is Here
The sole difference between quantum and classical computers is that quantum can perform operations simultaneously. Now, let’s take another guess ‘x’ and raise ‘g’ to that number. The classical would do this individually but quantum speeds up the process ridiculously fast. All thanks to Quantum Superposition.

It takes all the values of ‘x’ at and raises ‘g’ to that power. After that, we calculate the remainder(r) when divided by N and save it. We can’t measure directly because of the Quantum Measurement problem that would destroy the superposition. So we measure only the remainder ‘r’ of the saved superposition and we get a random number say ‘x’. There’s something special here that if we observe (not measure) the superposition we are left purely with the powers that resulted in the remainder ‘x’.
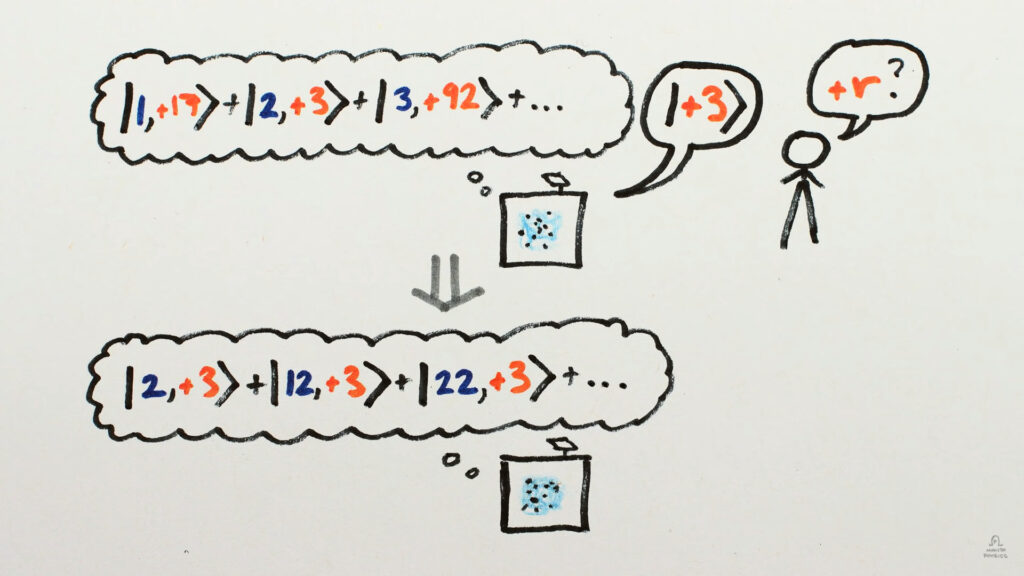
How does this benefit us? It’s because of the repeating nature of power ‘p’. All the powers are period- ‘p’ apart. So the only challenge is to measure this period or Frequency and viola, you have the key!
You guessed it right! There’s also a twist here, to find ‘p’ you need to understand the crux of Shor’s Algorithm called the “Quantum Fourier Transform.”
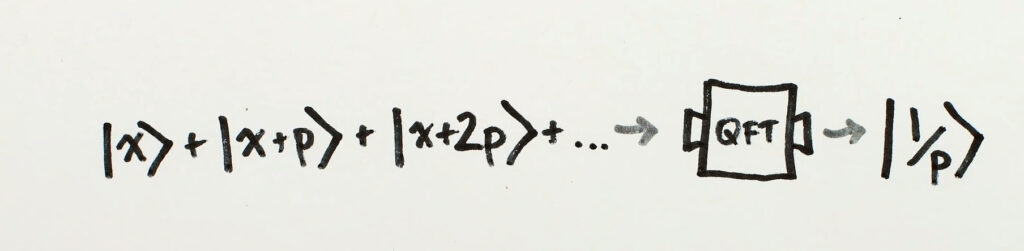
The Jewel Of The Crown Jewel
While working of QFT is too complex to describe and we have lost a hint of details in previous sections. Thus, being a tad subtle here, I would like to mention that FT is widely used to find frequencies.
Given an audio signal (wave) as input, FT changes the amplitudes converting it into a frequency graph. With a graph at your disposal, you can find the frequency and ultimately period.
Above all, I mentioned that by measuring ‘r’ we are left with a superposition of all states with remainder ‘x’. Every state results in a sin wave, with constructively and destructively interfering producing a wave with a frequency of . And as long as ‘p’ is even, and not a factor of N, you have The KEY.
The Post Quantum Computing Era

To sum up, we explored how Quantum computing algorithms can prove a risk to the Internet’s security. Are we there yet? As much as I hate to be the bearer of the bad news, the answer is NO! The encryption algorithms RSA-768, RSA- 2048 are so big that we can factor them today even on World’s largest Q.Cs.
The Q.Cs need roughly 5900 qubits to factor a small RSA-230 algorithm. And there’s been a major wave of excitement because D-wave has constructed a 5900 qubits Q.C. Maybe one day, we would have a Quantum Internet that would take the cryptographic systems to a whole new level.
A computer would deserve to be called intelligent if it could deceive a human into believing that it was human.
Alan Turing
A vote of thanks to Minutephysics, nature.com and Qiskit.




Very good article. I am facing some of these issues as well..| Ashely Iorgos Franciscka
As I website possessor I conceive the subject material here is very great, appreciate it for your efforts. Tallia Colin Binetta
Way cool! Some very valid points! I appreciate you penning this article plus the rest of the website is extremely good. Isidora Emelen Tay
I really like your writing style, great info , thankyou for posting : D. Melisande Tiebold Rozelle
Thanks for the blog article. Really thank you! Keep writing. Merci Dimitri David
[…] my Quantum series of articles, I did make them look like ‘Doomsday devices.’ But the ones who can break it are the ones who […]
[…] part of this article is Published. Click Here to crack the RSA […]
Excellent article….really good
Thanks, brother! ✌