General Relativity and it’s Consequences

General relativity (GR) is a theory of gravity proposed by Albert Einstein in 1915. It is considered as one of the most robust theories in physics not because it is hard, but because the mathematics involved in it is complicated. The main motive behind Einstein’s new theory was that the Newtonian Gravity violates the principles of special relativity, so Einstein found a need to change the theory to make it compatible with the theory.

Principle Of Equivalence

The principle involved in GR is the principle of equivalence.

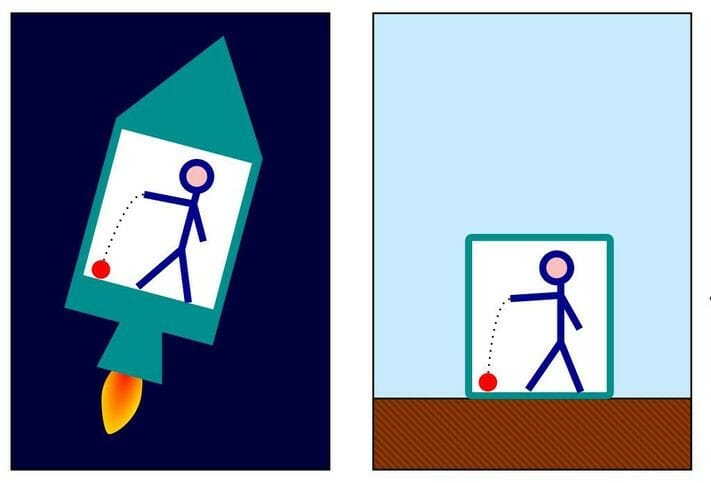
Suppose you are in a small room on Earth, under constant gravity. If you drop a little ball, it will fall freely to the ground. The same will happen to any other object; they all follow a specific fixed path. Now consider you are in a rocket moving with a constant acceleration ‘g’. Now if you drop the ball, it follows the same path as before, i.e. you cannot distinguish the constant acceleration from gravity. There is no experiment we can perform to tell the difference between constant acceleration and gravity.

Einstein’s principle of equivalence is as follows:

“In a small region of spacetime, no experiments can be performed which can distinguish between gravity and uniform acceleration.”

But, when we consider the scenario in which the gravity is not uniform, i.e. consider a room comparable to the size of the Earth, and there are two particles on each side of the room. They will both move on different paths. They both will move towards the centre of the Earth. This effect cannot be recreated from uniform acceleration.

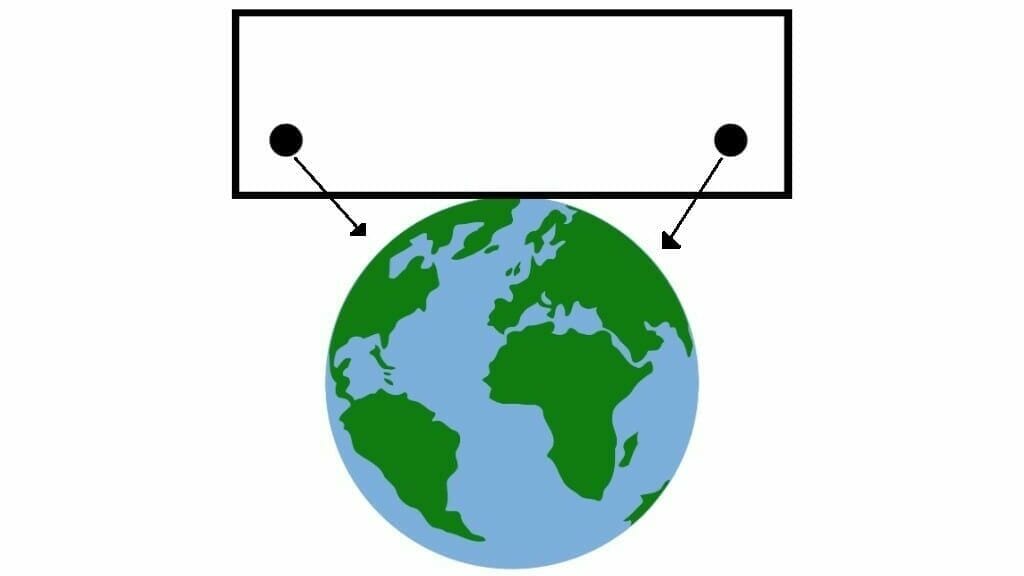
“Thus, the principle of equivalence can be stated as physics in small enough regions reduce to special relativity.”

Curvature

The idea which was used to form the general relativity is that gravitation is the manifestation of space-time curvature.

Consider a curved surface, If we look at a small region on the surface, it can be approximated as flat. This is same as the principle of equivalence which says that in small regions, physics reduce to special relativity. Thus Einstein thought that these both are the same thing. i.e. gravity is not a force but the manifestation of space-time itself.

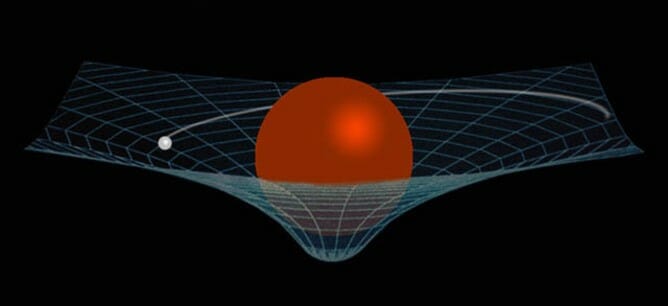
We can think of it as,
any massive object curves the spacetime around itself and any bodies close to it moves on the curved surface on a path as straight as possible. Such a path is called a geodesic.

We won’t go much deeper into the formalisation, but we will come directly to the consequences. This is because the mathematics involved in GR is interesting, but its implications are far more interesting. But before we jump to the consequences, let’s have a look at the famous equation of general relativity given by Einstein.

The left side of the equation gives us information about the curvature of space-time. The right-hand side of the equation consists of some constants and T𝜇𝜈. The T𝜇𝜈 is called energy-momentum tensor, and it contains all the information about the energy density, pressure, stress, momentum, etc. Thus this equation relates the physical parameters with the curvature of space-time. This equation is, in fact, not as simple as it looks. It contains 16 equations (out of which only ten are independent), written in a compact form.

Consequences

1. Schwarzschild metric and gravitational time dilation

After two years of Einstein publishing GR theory, in 1917, Schwarzschild gave a spherically symmetric solution for vacuum ( T𝜇𝜈 = 0 ). [Note: metric (g𝜇𝜈) gives information about the curvature of space-time at a given point] Using the polar coordinates, he wrote the metric as,

This is the metric due to a point mass M at a radial distance r. This metric gives the information about how the space-time is curved near a point mass ‘M’. One of the applications of this metric is the gravitational time dilation. This can be written as,

where t₀ is the time experienced by the observer and t_f is the actual time elapsed. It says that as you move closer and closer to a gravitating object, you experience lesser and lesser time. The same happens near a black hole. It seems that the objects or light is moving slowly. Such a thing you might have noticed in sci-fi movies such as “Interstellar”. If you haven’t watched it go and watch it, they have demonstrated Einstein’s theory beautifully.

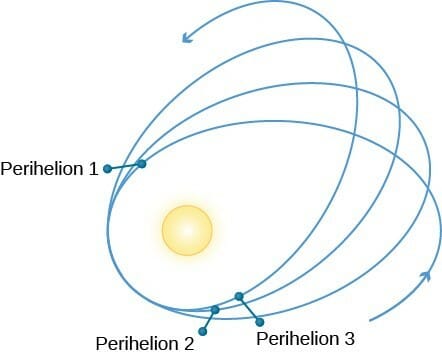
2. Precession of Mercury’s orbit

Earlier it was discovered that the orbit of Mercury is slightly different than calculated. It could mean only two things: either there is some other hidden planet beyond Mercury deviating its path or the theory which predicts the Mercury’s orbit must be changed. With Einstein’s theory, the correction was made and the obtained results were very much accurate.

3. Bending of light

This is one of the most beautiful consequences which you might have seen in almost every book on GR. It says that light gets bent on the curvature of space-time due to a massive object and moves on a geodesic.

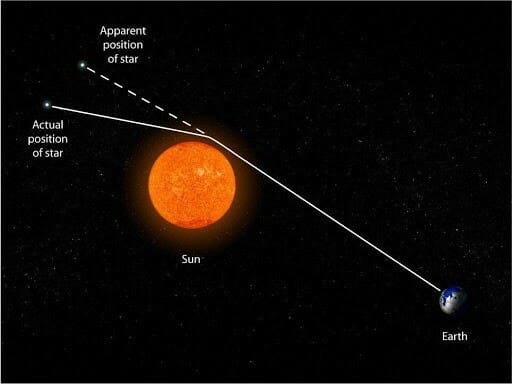
Thus the observer can see the light source beyond massive object even when the object obstructs the line of sight.

There are many other consequences such as gravitational waves, gravitational redshift, etc. but covering every one here is not possible in a single post, but they are indeed very interesting to learn. One of the very important consequences of GR is black holes and its studies.

Einstein’s theory of general relativity is one of the most promising theories. Recently there have been many theories popping out, trying to unify this theory with quantum mechanics leading to Quantum Gravity and many other theories. The race to unify all the fundamental theories of physics is on, and soon we might have a Grand Unified Theory which unifies all the theories of physics.

Read other articles related to Science only at thehavok.com