Subscribe
Home Blog Page 8

Black Holes, Entanglement And Wormholes

Vibhor Singh
-
4
Black Holes, Entanglement And Wormholes

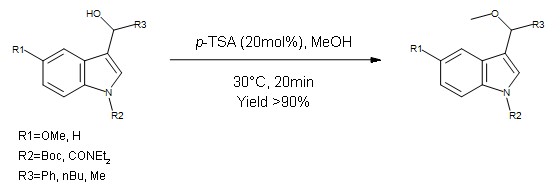
Black holes are highly gravitating objects concentrated at an extremely small region. The study of a black hole is the study of Quantum Physics and General Relativity (Gravity).

Let’s talk about black holes first.

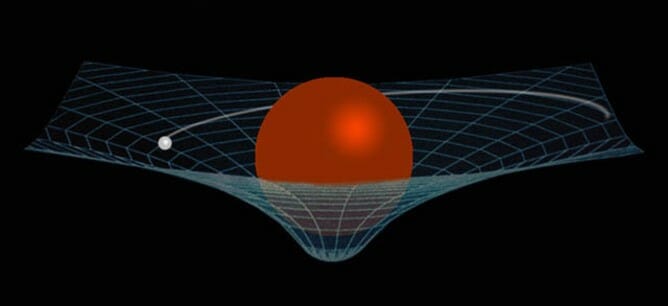
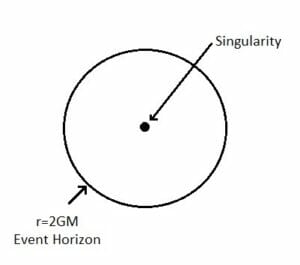
For a black hole of mass M, the radial distance r = 2MG is known as “Event horizon”. It is that distance from which nothing, not even light can escape. If you are inside horizon you are doomed. You will eventually fall into the centre of black hole which is known as “singularity”.

Black Hole

Einstein’s GR talks about gravity in terms of the curvature of space-time. So, let’s see what we can say about black holes in terms of GR we already know.

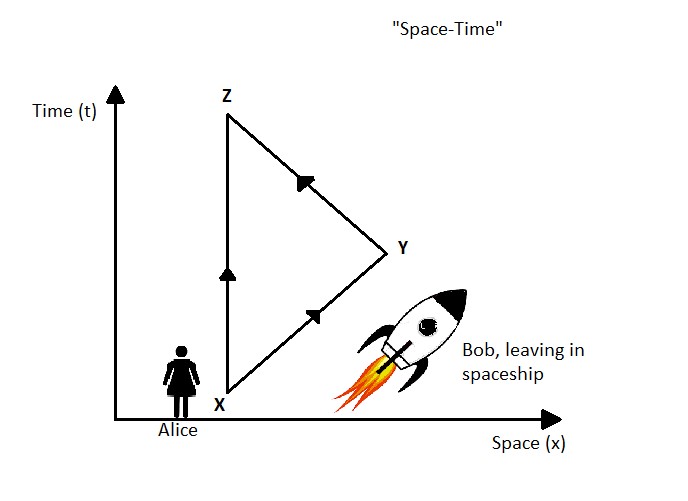
Suppose there are two people: Alice and Bob. Let’s say Bob jumps into the black hole, sacrificing himself for science, and Alice stays at some distance and watches him. From special relativity, we already know that the time experienced by both of them will be different.

So, let’s see what both of them observe when they are far away from the horizon. As Bob is falling into the black hole, he will not see anything peculiar. But Alice sees that Bob is slowing down as he moves towards the horizon. This is due to gravitational time dilation.

\Delta t^{^{'}}=\Delta t\sqrt{1-\frac{2GM}{rc^{2}}}

Where t is the time experienced by Alice, and t’ is the time experienced by Bob. We can see that as r decreases, 𝚫t0 increases. If we put r = 2MG, 𝚫t0→ ∞ i.e, Alice will see that it will take infinity time for Bob to reach the horizon. Alice will see Bob slowing down, but never reaching the horizon.

Also, another effect, the length contraction, comes into play, and Alice sees Bob’s length getting shortened as he will move towards the horizon. So what Alice observes is that Bob’s length gets contracted and he is slowing down as he reaches the horizon, but for her, Bob never reaches the horizon, he is squished into an infinitesimally thin layer without even reaching the horizon.

But coming to Bob, he will never experience anything peculiar, and just normally falls into the black hole.

The solution to Einstein’s field equations says that the geometry of space-time near the horizon is smooth. So Bob necessarily does not experience anything weird. But once he is inside the horizon, no matter how hard he tries, he cannot escape falling into the singularity Even if he moves radially outwards, he will follow a spiral path and eventually meet singularity. Gravity there, is so strong, that even light can’t escape out.

Thus it can be said that the event horizon is a point of no return.

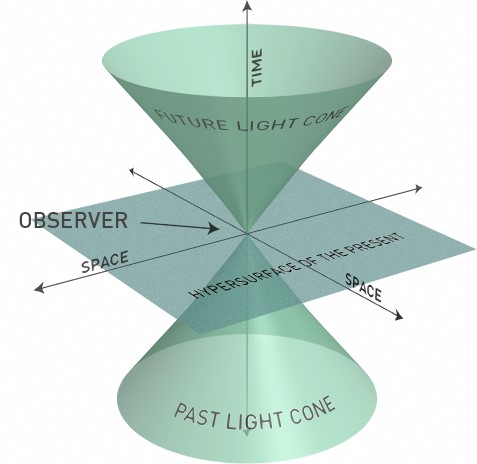
One of the best ways to describe all these processes through a diagram is using Kruskal-Coordinates. Getting used to them is a bit difficult but we’ll see.

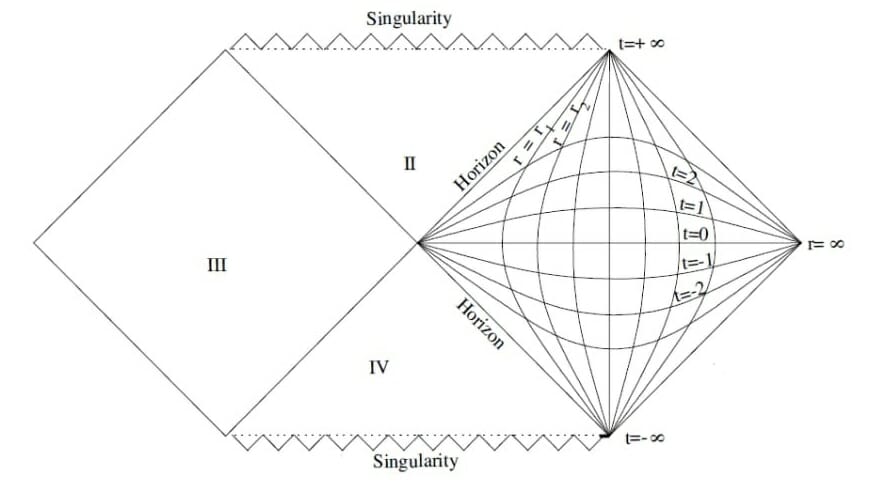
Quadrant I is the exterior of black hole and the big cross at the centre is the horizon. Quadrant II is the interior of the black hole.

If you draw lines at 45 degrees, that will represent the path taken by light and any other massive particle will take a path inside that region.

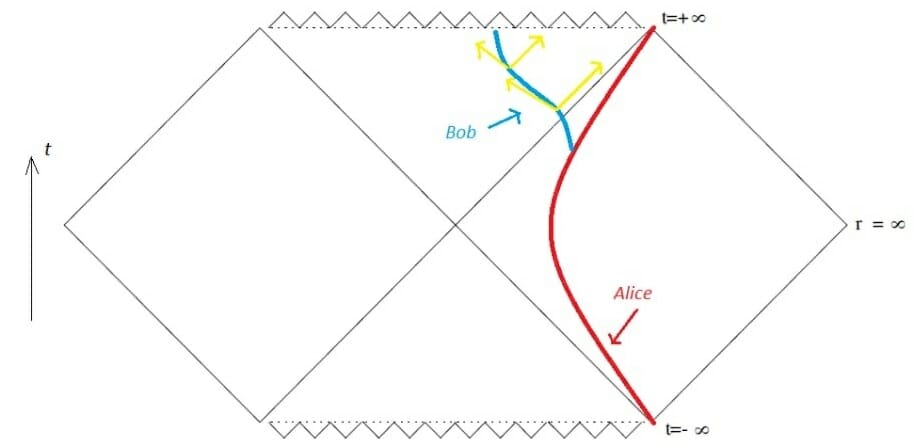
As you can see from the diagram, when you are inside the horizon, you cannot draw any lines which allow you to go back to the Ist Quadrant. The only place where you can go to is the singularity. From the diagram, it looks as if the singularity is not a place but a moment in time because it looks like the time slices t=0,1…etc.

So as we can see from the diagram, Bob will eventually meet the singularity.

Let’s talk about entanglement for a while. Entanglement is the backbone of quantum physics. Let’s take an analogy. Suppose we have 2 pebbles, one red and one blue. We give one to Bob and one to Alice without telling them which one is which and send both of them far away from each other, say 1 light year. Now if Bob looks at his pebble and sees that he has a blue pebble, he instantly knows that Alice has the red one. This sort of correlation is called entanglement.

The point of interest is that the vacuum is entangled. The vacuum we see is not empty. It seems senseless but let us put some sense to it.

Imagine a region of vacuum and divide it into two segments by a partition.

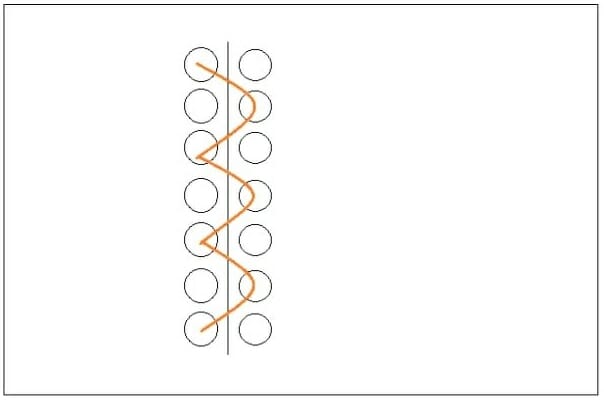
What we mean is, the vacuum is composed of different fields. There might be energy fluctuations inside it causing an electron-positron pair to form. So if we look at a small region on the left side, and we find a particle present, then we will know that there is another particle on the right side, and vice versa. This is because the vacuum is entangled.

Entanglement is what binds the universe together, and is the key to the isotropic nature of the universe.

Now coming back to the Kruskal coordinates, we had left out the Quadrants III and IV. They are part of another black hole which s somehow connected to the first black hole.

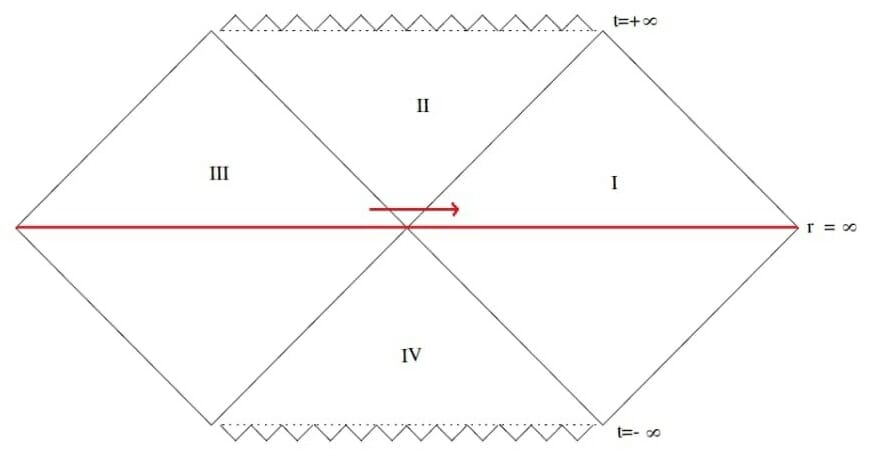
If we somehow manage to move horizontally from Quadrant III to I (do note that physics does not allow this, as this requires moving faster than the speed of light), we’ll move from one black hole to other, even if these are separated by a huge distance in space, i.e. both black holes are connected somehow. And this connection is called a “wormhole” or Einstein-Rosen bridge.

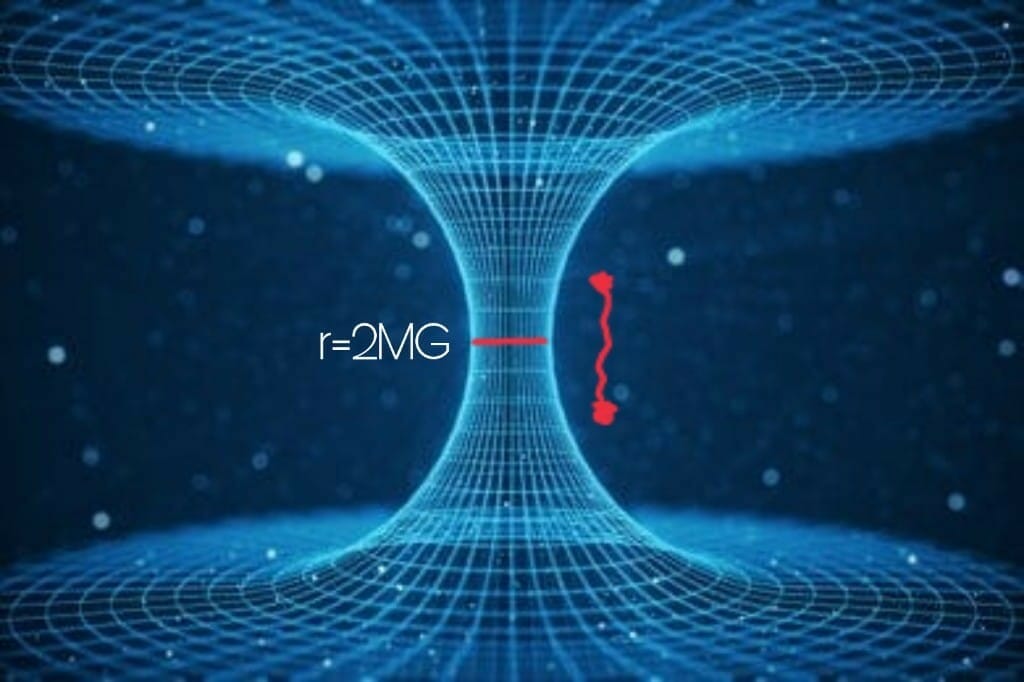
From the Kruskal-coordinates, we see that the geometry is smooth moving from one black hole to another, i.e. nothing is there except space inside the wormhole. But we already know that space is entangled. So now if we take a small region near the event horizon of each black hole, it is entangled.

Strictly speaking, these two black holes are entangled with each other. Entanglement is the thing that connects these two black holes which might be even 1000 light-years apart.

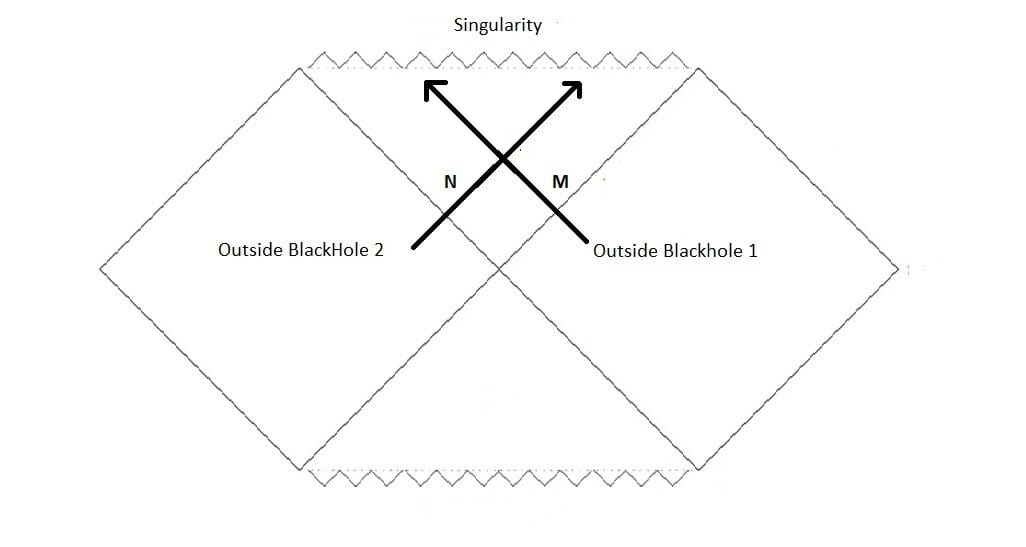
The two black holes are connected to each other by a small region of the event horizon. It looks as if we go inside one, we end up coming out of the other as seen from the diagram. But in reality, once we enter the event horizon, we do not have enough energy to come out of it. The only thing that is possible is, suppose we have two particles, say M and N going inside from each black hole, they both will meet at the entangled region of the horizon.

The same thing can be understood from the Kruskal coordinates.

I.e. they can only meet inside the horizon and they both will meet at the singularity.

Thus, black holes are the topics of utmost importance for both general relativity and quantum physics. There are many paradoxes about black holes, some solved and some yet unsolved.

The Big Bang & the Universe

Keith Kamson Fernandes
-
12
The Big Bang & the Universe

The Big Bang Theory is the currently the most accepted explanation behind the beginning of the Universe and the current standard cosmological model (Lambda-Cold Dark Matter or Lambda-CDM model) is based on. Thought the Big Bang Theory doesn’t give us the whole explanation of the Origin of the Universe. It explained that the Universe started with a Big Bang or you say singularity about 13.82 billion years ago. Though we fully don’t know how it happened, we are able understand it through mathematical equations and models.

Timeline of the Big Bang

1. Singularity & Inflation

The Universe was born due to a gravitational singularity (which is when a point in space-time where the gravitational field of the body becomes infinite as predicted by General Relativity). Though this an irregular behavior which we do not have an adequate understanding of it.

According to the theory, when the Universe was born it was very dense and very hot. The singularity is also known as Planck Epoch or Planck Era. During this period, all matter was condensed on a single point of extreme heat and infinite density. It was also believed that the quantum effects of gravity dominated physical interaction and gravity was the strongest as compared to the other physical forces.

Timeline of the Universe based on the Big Bang Theory
Timeline of the Universe based on the Big Bang Theory (Image: NASA/WMAP)

Inflation started at 10-32 seconds, after the creation of the fundamental forces of the Universe. The Inflation continued up to a unknown point, which most cosmological models suggest that it continued until the Universe was filled with a high-energy density and that the extremely high temperatures and pressures gave rise to cooling and expansion of the Universe

When the Big Bang occurred, the temperature surrounding at the very first second was about 5.5 billion Celsius (or 10 billion Fahrenheit) with formation of neutrons, protons, electrons, photons, positrons (anti-electrons) and neutrinos with the number being more than 10 billion degree (i.e. 10^10). However, as time passed by, it was seen that the Universe cooled down, neutrons and protons combined to form an isotope of hydrogen deuterium.

2. Cooling & Structure

As the Universe continued to cool down, it reached the temperature at which electrons could combine with nuclei to form neutral atoms. Before this, the Universe was undergoing Inflation, where at the start the Universe appeared to have been opaque because free electrons would cause photons (light) to scatter. However, when the free electron were seen combining to form neutral atoms, the Universe started to become transparent. Those same photons are now the afterglow of the Big Bang is now known as Cosmic Microwave Background (CMB), which is known as the oldest light in the Universe. Though as the CMB expanded, it gradually lead the Universe to lose density and energy.

Cosmic Microwave Background of the Universe, where red are the heat spots and dark blue are the cold spots
Cosmic Microwave Background of the Universe, where red are the heat spots and dark blue are the cold spots (Image: NASA/WMAP)

As time passed by which was about a few billion years, the denser region in the almost uniformly distributed matter of the Universe started to get gravitationally attracted to each other. This attraction between the matter lead to the formation of gas clouds, stars, galaxies and all the other astronomical bodies we see today. As visible matter was formed, more suggested types of matter was formed which was cold dark matter, warm dark matter, hot dark matter and baryonic matter. However, the Lambda-CDM Model which is considered the standard model of Big Bang, has dark matter particles fit in as it matches with the available data.

3. The Present Expanding Universe

The present Universe we are in is currently dominated by a mysterious form of energy called Dark Energy. Observations suggest that it compromises about 73% of the total energy density of the present Universe. It is suggested that when the Universe was formed, it was infused with dark energy, but due to less space and everything was close together, gravity dominated dark energy and it was slowly barking the expansion. But as time passed with Universe expanding, the growing amount of dark energy caused the expansion in the Universe to slowly accelerate.

History of the Big Bang

The word “Big Bang” was coined by English Astronomer Fred Hoyle during a talk for BBC Radio in March, 1949, quoting that: “These theories were based on the hypothesis that all the matter in the universe was created in one big bang at a particular time in the remote past.”

In the early 20th century, most of the astronomers believed that the Universe was static saying that nothing new was added and the size didn’t change.

The first evidence proving that this so-believed “static model” was wrong came in the form of a discovery by an American astronomer Vesto Slipher in 1912. When he was measuring the Doppler Shift (which is the change in frequency of a wave in relation to an observer who is moving relative to the wave source) of a spiral galaxy and discovered that the almost such galaxies were receding from Earth.

A decade later, Russian physicist Alexander Friedmann derived the Friedmann equations from Albert Einstein’s field equations, showing that the Universe was expanding rather than static as stated by Einstein. In 1924, American physicist Edwin Hubble added details to the measurements done by Vesto Slipher by providing distances and later Belgian physicist Georges Lemaître showed evidence that the Universe was expanding which gave rise to Hubble- Lemaître Law or famously known as the Hubble Law which gave a correlation between distance and recessional velocity.

In 1968 and 1970, Roger Penrose, Stephen Hawking, and George F. R. Ellis published papers where they showed that mathematical singularities were an initial condition of relativistic models of the Big Bang.

This diagram shows how Hubble has revolutionised the study of the distant, early Universe.
This diagram shows how Hubble has revolutionised the study of the distant, early Universe. (Image: ESA/Hubble)

Later in the late 1990s, there was seen a huge progress in the theory due to telescopes and as well as analysis of data from satellites such as Cosmic Background Explorer (COBE), Hubble Space Telescope and Wilkinson Microwave Anisotropy Probe (WMAP).

Coffee stain inspired printing technique: All you need to know

Om Desai
-
2
Coffee stain inspired printing technique: All you need to know

Once in a lifetime each of us have spilled coffee on our desk or workplace or at any other table. It creates a coffee stain, which everybody wipes out, thinking of nothing. But these coffee-stains develop because one of the most puzzling phenomena of Fluid Mechanics. This was called to be the “Coffee-ring Effect”. The same thing happened with Cambridge, Durham and Beihang University researchers and they produced most innovative concept of printing for fabrication of electronic devices. This effect, enabled the low-cost manufacturing of electronics with the help of coffee stain inspired printing technique. Some of these electronics are sensors, light detectors, batteries and solar cells, from Ink-Jet technological innovation.

Before going further, lets briefly know what is this puzzling “Coffee-Ring effect”.

The “Coffee-Ring Effect”:

coffee ring effect
Coffee Ring Effect (Image: ScienceAdvances)

Don’t get confused if you can’t understand the picture (its technical 😊). Simply we can say that, the liquid at the edges evaporates faster than on the inner side. This rapid evaporation induces flow inside droplet due to difference or gradient in surface tension (this can be observed in above figure at last). It is know as Marangoni Flow. Because of this, free surface at the edges get collapsed and liquid is trapped from the inner side of coffee stain. This flow induced towards the edge, carry almost all dispersed material rapidly at the final stage of drying process.

With this, if there is interaction of suspended particles of droplets with its surface, then only this effect is observed. At top of figure, inverted optical micro-graph of dried inkjet droplets on clean glass. Thus, in one line, it can be said that, coffee stain rings form because solid particles accumulate after the quicker evaporation of liquid from edges (this can be observed in middle part of above figure, with example of butanol).

Application in coffee stain inspired optimal printing solution:

Now knowing what is the phenomena of printing technique for electronics, lets understand how its done. Researchers observed that while printing on hard surfaces, inks accumulate at the edges creating uneven surfaces and irregular shapes. This damages whole printing process. But one thing noted here was, this was the same behavior as observed during the formation of coffee stains. This led into deep study on physics of ink droplets. It was done by combining particle tracking in high speed micro-photography, fluid mechanics, and different combination of solvents. Many conclusions, trial and errors, confirmations were made based on that study.

But among those, they prepared a solution/mixture of alcohol. To be specific, it was a solution of isopropyl alcohol and 2-butanol.

isopropyl alcohol
2- butanol

When mixture of these compounds was used, it was observed that ink particles distributed evenly across the droplet. Meaning, they also have shown coffee-ring effect, but in a systematic and even manner. Unlike the usual inks used in inkjet printers, they didn’t spread unevenly. But accumulated systematically, providing properly printed smooth surface even at edges. This led to coffee stain inspired optimal printing technique for fabrication of electronics.

One of the researchers said that, “The natural form of ink droplets is spherical — however, because of their composition, our ink droplets adopt pancake shapes.” This helped them to fabricate the printing electronic devices like sensors, photo-detectors, wearables, spray printing and many such inkjet printed devices.

They also observed that while drying these new ink droplets they deform across the surface smoothly. This leads to even spreading of particles and increases consistency. Along with this, they also avoid the addition of commercial additives like surfactants and polymers. This makes them more environment friendly and cheaper to get. Thus, with most common phenomena neglected by almost everyone, they made most efficient way of printing technique for fabrication of electronic devices.

Advantages of this printing technique inspired from coffee stain:

The coffee stain inspired printing technique has laid upon the foundation of high-speed additive manufacturing of all printed sensors. At the same time, it also helped large scale fabrication of systems requiring huge amount of large-scale integration.

Inkjet printing of such 2D-crystals enables scalable device fabrication. This device fabrication can be achieved with high consistency and reproducible properties.

Further, when this mechanism can be understood, more solvents can be adapted to opt for more applicability. This increases the acceptance of the technology in wider areas and more industrial reach can be obtained.

drying droplets
Particle trajectories of drying droplets, with red arrows showing the trajectory end. (Image: University of Cambridge)

Also, it is now applicable in the areas of 2D crystals, nano-particles, organics and other different material platforms. Just now fabrication of complex devices is tough and costly. This technology can provide reliable printing of wide range of optically and electrically active materials and their mixtures. With that, there can be boost in production of complex emerging devices and at subsequently low costs.

This technology also has shown excellent consistency, scalability and reproducibility. Previously, printing of few hundred devices was considered success even with uneven behavior. But, this newest technology can be opted for the printing of electronic devices on silicon wafers or plastics.Using this technology, researchers have manufactured nearly 4500 identical devices on silicon wafer and plastic substrate. With more and more demand for printed devices in the market, current manufacturers are not able to fulfill needs. Usage of this technology enables them to scale-up inkjet printing of all kinds of 2-D crystals. Which means that, in future, needs of market can be matched easily at cheaper costs.

Future scopes:

Researchers expect sooner and reliable application of technology for industrial purposes. Their technology can be considered a game-changer and help companies and industries to grow in the field of printed devices.

Some of the successful attempts for the application of this technology are printed sensors and photo-detectors. They have shown promising results in terms of sensitivity and consistency. Naturally, with these results, future of printed and flexible electronics will be flourished. This is because, coffee stain printing technique provides results exceeding the current industrial needs yet are low cost and efficient. This perfectly makes them suitable for electronics industry.

In short, with this technology, dreams of smart cities will come true, at a way cheaper and yet inexpensive manner. Lastly one can say that, this innovation is best example of creation of most useful technology from most ignored stain of everyone’s life.

So next time in your life, you better not wipe your stains out.

— OSD

The Story of GOD (particle) – The Higgs Mechanism

Adithya A Rao
-
0
The Story of GOD (particle) – The Higgs Mechanism

Higgs Boson holds the honour of being the most renowned particle of this century. The announcement of its detection by CERN in 2013 prompted the whole world to rejoice. Articles glorifying this ‘God Particle’ crowded the pages of all newspapers. The physics world celebrated; everyone was speaking about it everywhere. Although, only a very few understood what the Higgs Boson was, or why the evidence of its presence is vital for theoretical physics. 

Why Higgs Mechanism?

It is a fascinating fact that all of physics can be narrowed down to symmetries*. A very peculiar symmetry, the gauge symmetry*, is used by the standard model to describe the fundamental forces of the universe, except gravity. In explaining the electromagnetic and strong nuclear force*, physicist found an exceptional deal of success. Engrossed in this success, they raced towards constructing the gauge-invariant theory for the weak nuclear forces*. But in no time, they stumbled and fell facedown, crushed by consistent failure, with all the assumptions pointing to the bosons having zero mass. It was a cause of humiliation because these bosons were, in fact, massive, being 80 times heavier than protons. 
What this implied was that either the gauge-invariance was the faulty procedure, or there was something else – something unknown to physicists – that was providing mass to these bosons.

[Words marked * are defined/explained in glossary]

The answer…

In the 1950s spontaneous symmetry breaking was found to be possible under specific physical circumstances. What this meant is that a system having symmetric Lagrangian* in higher energy states can violate these symmetries in low energy near-vacuum states. Thus even an asymmetric system could have a perfectly symmetric Lagrangian. This spontaneous symmetry breaking suggested that the Gauge symmetry could be broken. But for this, a bizarre field* was needed to be omnipresent throughout the entire universe. This field is bizarre because all other fields have zero value in vacuum, but this specific field had non zero value everywhere. This very field was called the Higgs field, and the mechanism which led to the symmetry breaking was called the Higgs mechanism. 

spontaneous symmetry breaking
Explanatory diagram showing how symmetry breaking works. At a high enough energy level, a ball settled in the centre (lowest point), and the result has symmetry. At lower energy levels, the centre becomes unstable, the ball rolls to a lower point – but in doing so, it settles on an (arbitrary) position and the result is that symmetry is broken – the resulting position is not symmetrical.
(Image: Wikipedia)

How the Higgs Mechanism can be thought of…

A very elegant parallel can be devised to explain the Higgs mechanism.  
Picture a lamp lit in a vast open field in the nightfall. This lamp is to be thought of as the source of the force, and the light rays as lines of force. The farther you walk from the lamp, the light you receive gets dimmer, certainly obeying the inverse square law. The lamp would always be faintly noticeable even at a considerable distance. You can take this to be analogous to the electromagnetic force. The force transmitting bosons, the photons are massless and can travel to infinite lengths.

light rays in open field
The light rays in travel endlessly unaffected by anything
(Image: Sean Carroll)

The strong and weak nuclear force both are short-ranged forces. The short-range would require the lamp to be brightly visible closeby and to be swiftly fading away. Nature provides two plausible arrangements for the same. 

One, consider an enclosure or a cabin with the lamp installed inside it. The lamp is brightly visible inside this cabin, but the instant you step out, the lamp is obstructed from your sight. This process is called confinement, and the strong nuclear force reflects this approach. The strong force-carrying bosons, the gluons are massless. But they interact with each other so strongly that they are confined to such a small region.

confined light rays
The light rays never leave out the confined region, thus being limited to the small area.

The second approach is to conceive of a veil of dense smog enveloping the whole field. The farther you go, more the light rays are absorbed, and the lamp gets shadowier swiftly. Thus in regions close to the lamp, you can see it bright. But the moment you walk a distance, the light from the lamp is wholly absorbed. Thus the lamp is not visible anymore. 

attenuated light rays
The light rays are absorbed by the surrounding smog thus being limited to a very small region depending on the density of the smog

You can conceive this smog as the Higgs field that permeates the entire universe. This field is attenuating the weak force bosons making them short-ranged. If the bosons were massless, they would have infinite range and would have been able to travel at the speed of light. But now, thanks to the Higgs field, they break out of symmetry requirements and gain mass, and this makes them short-ranged.

The Higgs field was initially devised to explain the short-range and heavy masses of weak force carriers. But later on, it was discovered that this field also gave mass to most of the elementary particles. Thus the Higgs field became the mass giver for the standard model.

The Higgs Mechanism and the Higgs Boson

The Quantum Field Theory – QFT explains the universe in terms of fields. According to it, all particles are excitations of their respective fields. Electron-of the electron field, quark of the quark field and so on. Similarly, the Higgs Boson is the excitation or instance of the Higgs field. And confirmation of the existence of the Higgs Boson confirms the Higgs field theory. This is very important for the progression of theoretical physics because it explains the weak forces, the ones responsible for nuclear fusion fueling all the stars. This is the reason the whole physics world breathed a sigh of relief when LHC, CERN announced the detection of Higgs Boson in 2013.

The Higgs Boson at CERN
Representation image showing the reaction that led to birth of Higgs Boson in LHC
(Image: CERN)

Higgs Boson in Pop Culture…

The Higgs Boson has been referred to as “God particle” extensively in pop literature. Many movies and TV shows have glorified it, giving it qualities it never even intend to possess. The name “God particle”, which grants a mystical feel to the particle, itself is an accident. It can be traced back to Nobel prize winner Leon Lederman who intended to write a book titled “The Goddamn Particle”. The name was meant to make fun of how hard the particle was to detect. But the publishers objected on this and instead replaced “goddamn particle” with “god particle”, the name which stuck on forever, to the annoyance of most physicists.

The Higgs theory has led to several daughter theories trying to explain eccentric physics results. The fact that dark matter has mass implies that it would interact with the Higgs Boson. There are also theories proposing that the Higgs Boson could decay to form dark matter. Thus the evidence of Higgs theory in 2013 has directly solidified our search for the physics beyond the standard model.

GLOSSARY:

Symmetry: The laws of physics do not change under certain conditions, like moving forward or backward in space or time, rotations in space, and many more. This property is called symmetry.

Lagrangian: It is a function that describes the state of a system completely. It is written in terms of positions and velocity and it is enough to describe the whole system.

Gauge Symmetry: When the final equation of state does not change upon adding few derivatives to its Lagrangian, it is called gauge symmetry.

Field: It is a physical entity that is assigned to every point in space-time, whose values change with the position.

Strong Nuclear force: The force that holds together quarks inside the protons, neutrons and other entities.

Weak Nuclear force: The force that acts between subatomic particles, and is responsible for their radioactive decay.


Carbon Dioxide: Can a Greenhouse Gas Meet Energy Needs

Umakant Bohara
-
4
Carbon Dioxide: Can a Greenhouse Gas Meet Energy Needs

“Carbon dioxide” this word brings images of pollution, industrial waste, climate change, global warming to our mind, but we are at the beginning of an era where we will have a different perception of the ongoing energy crisis, all thanks to the scientific innovations in the field of energy sciences and engineering. From air capturing technology to CO2 recycling, many such advancements are on their way to bring about a revolution and overthrow the traditional energy sources.

Utilizing the excess carbon dioxide which is a by-product of major industrial processes could do wonders if not simply released or disposed at the ocean beds. Several research projects are being undertaken to develop an effective technique to direct CO2 emissions towards various energy storage based projects.

Following are some cutting edge projects and discoveries that deploy not so eco-friendly carbon dioxide gas:

Ethanol synthesis using Copper based electro-catalyst

Scientists from Argonne National Laboratory claim to have build a catalyst that recycles CO2 into energy-rich ethanol. Further, this process can be powered by renewable energy. This method has an efficiency of nearly 90% which is more than any other industrial process known. Synthesis of ethanol is just one process out of the possible long list of recycling CO2 into other useful chemicals.

Breaking chemically stubborn carbon dioxide at low energy cost can pave the way to multiple ways of producing useful chemicals and can start a domino effect of new discoveries in the field of energy sciences. The most immediate opportunity that would open up is converting CO2 into hydrocarbons. These processes can be so efficient that the mitigation of CO2 at the bedrock will have to find its way out.

What makes this catalyst so magical is its composition. The catalyst consists of atomically dispersed copper on carbon-powder support. Under an external electric field, an electrochemical reaction is initiated in which catalyst breaks down CO2 and H2O molecules to selectively reassemble the broken molecule into ethanol. The electrocatalytic efficiency (Faradaic efficiency) is close to 90%.

(Image: Larry Curtiss)

The research was benefitted from the facilities like the Advanced Photon Source (APS) and Centre for nanomaterials (CNM) which has the Laboratory Computing Resource Center (LCRC). The high photon beam at APS helped in detecting the structural changes in the catalyst during the electrochemical reaction. A high-resolution electron microscope at CNM and modeling at LCRC revealed the reversible transformation between atomically dispersed copper and clusters of three copper atoms each. This finding sheds light on further improving the catalyst by deploying rational design.

Scientists at ANL, now look forward to deriving new catalysts through a similar approach to convert CO2 into hydrocarbons. It has the potential to bring major reforms to the industrial world.

Direct Air Capture Technology

carbon engineering plant
(Image: Carbon Engineering)

What if we could extract CO2 from the atmosphere just like plants and trees. The answer is, we could have a solution to tackle climate change and bring about energy reforms. Industries, vehicles, power generators, and other human needs consume fuels to deliver the desired outcome and in turn release CO2 and other harmful gases. Scientists and industrialists took this environmental issue as an opportunity to stride towards carbon neutrality. Direct air capture technology is something that has been developed to create a loop to produce fuel out of CO2

Carbon Engineering is a company located in British Columbia that has a CO2 sucking and processing plant located between high cliffs and valleys. This plant uses giant fans (air contactor) present under the open sky driven by renewable energy sources to suck the air directly from the atmosphere. Pulled air then becomes a part of a series of chemical reactions to extract CO2 and release other gases back to the atmosphere.

Polymer sheets are placed such that air passes through the dripping potassium hydroxide. Again, this chemical solution has low toxicity and by exploiting the acidic nature of CO2, corresponding carbonate salt is obtained in the form of pellets which on heating release CO2 and remaining part of the salt is hydrated and returned to the initial form. Further, carbon dioxide collected is used in food processing or combined with hydrogen to obtain hydrocarbons and sold as synthetic oil in markets.

(Image: Carbon Engineering)

On a large scale, capturing a ton of CO2 costs them US$100. CE uses a combination of natural gas and renewable electricity to power its plant. CO2 emissions of natural gas are also directed to the system for capturing CO2. Their plant is capable of relying completely on renewable electricity but engaging it in a combination with natural gas cuts down the costs. Clearly, capturing CO2 has got zero-emission, in fact, a larger amount of it is being taken from the environment and is stored for further actions.

Being economically backed by Bill Gates, Chevron, and Occidental, CE aims to scale up and install plants in other parts of the world. However, not everyone approves this as a solution to tackle climate change or reduce CO2 emissions, professors from the University of Calfornia and Stanford University see partnering with oil companies is a wrong step and all this would promote fossil fuel usage instead of working in the direction of renewables. Investments in renewable energy harnessing projects like solar and wind energy could help more, environmentally, as these do not have the emissions in the first place.

What these projects do is not so complex and do not require traditional energy sources to operate on large scales. Each year the world emits about 40 billion tons of CO2, at this rate, it would take 40,000 such plants each capturing 1 megaton of CO2 per year. Many other companies based in different countries have already begun commercial air capturing. Political and technical scenarios associated with the direct air capture technology point towards a cleaner and greener future.

Lithium-Carbon Dioxide Battery

First Fully Rechargeable Carbon Dioxide Battery is Seven Times More Efficient Than Lithium Ion |

Lithium-ion batteries have found their use in multiple domains. From electric vehicles to mobiles, laptops, and other handheld devices, all run on lithium-ion batteries, and what makes it so ubiquitous is its energy density and recharging frequency. Energy sciences is a domain that has thousands of people engaged to find the most suitable devices that have capabilities to meet ever-increasing energy needs.

Researchers at the University of Illinois, Chicago have tested a design of lithium-carbon dioxide battery prototype which can be recharged completely and run efficiently even after 500 consecutive cycles of charge-recharge process.

Read further about Lithium-Carbon dioxide battery and new innovations in here.

General Relativity and it’s Consequences

Vibhor Singh
-
13
General Relativity and it’s Consequences

General relativity (GR) is a theory of gravity proposed by Albert Einstein in 1915. It is considered as one of the most robust theories in physics not because it is hard, but because the mathematics involved in it is complicated. The main motive behind Einstein’s new theory was that the Newtonian Gravity violates the principles of special relativity, so Einstein found a need to change the theory to make it compatible with the theory.

Principle Of Equivalence

The principle involved in GR is the principle of equivalence.

Suppose you are in a small room on Earth, under constant gravity. If you drop a little ball, it will fall freely to the ground. The same will happen to any other object; they all follow a specific fixed path. Now consider you are in a rocket moving with a constant acceleration ‘g’. Now if you drop the ball, it follows the same path as before, i.e. you cannot distinguish the constant acceleration from gravity. There is no experiment we can perform to tell the difference between constant acceleration and gravity.

Einstein’s principle of equivalence is as follows:

“In a small region of spacetime, no experiments can be performed which can distinguish between gravity and uniform acceleration.”

The Principle of Equivalence (Image: Forbes)

But, when we consider the scenario in which the gravity is not uniform, i.e. consider a room comparable to the size of the Earth, and there are two particles on each side of the room. They will both move on different paths. They both will move towards the centre of the Earth. This effect cannot be recreated from uniform acceleration.

“Thus, the principle of equivalence can be stated as physics in small enough regions reduce to special relativity.”

Curvature

The idea which was used to form the general relativity is that gravitation is the manifestation of space-time curvature.

Consider a curved surface, If we look at a small region on the surface, it can be approximated as flat. This is same as the principle of equivalence which says that in small regions, physics reduce to special relativity. Thus Einstein thought that these both are the same thing. i.e. gravity is not a force but the manifestation of space-time itself.

We can think of it as,
any massive object curves the spacetime around itself and any bodies close to it moves on the curved surface on a path as straight as possible. Such a path is called a geodesic.

General relativity
(Image: David Newman)

We won’t go much deeper into the formalisation, but we will come directly to the consequences. This is because the mathematics involved in GR is interesting, but its implications are far more interesting. But before we jump to the consequences, let’s have a look at the famous equation of general relativity given by Einstein.

R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }=8\pi GT_{\mu \nu }

The left side of the equation gives us information about the curvature of space-time. The right-hand side of the equation consists of some constants and T𝜇𝜈. The T𝜇𝜈 is called energy-momentum tensor, and it contains all the information about the energy density, pressure, stress, momentum, etc. Thus this equation relates the physical parameters with the curvature of space-time. This equation is, in fact, not as simple as it looks. It contains 16 equations (out of which only ten are independent), written in a compact form.

Consequences

1. Schwarzschild metric and gravitational time dilation

After two years of Einstein publishing GR theory, in 1917, Schwarzschild gave a spherically symmetric solution for vacuum ( T𝜇𝜈 = 0 ). [Note: metric (g𝜇𝜈) gives information about the curvature of space-time at a given point] Using the polar coordinates, he wrote the metric as,

g_{\mu \nu }=\begin{pmatrix} -1+\frac{2MG}{r} &0 &0 &0 \\ 0&\frac{1}{1-\frac{2MG}{r}} &0 &0 \\ 0& 0& r^{2}&0 \\ 0& 0& 0& r^{2}sin^{2}\theta \end{pmatrix}

This is the metric due to a point mass M at a radial distance r. This metric gives the information about how the space-time is curved near a point mass ‘M’. One of the applications of this metric is the gravitational time dilation. This can be written as,

t_{0}=t_{f}\sqrt{1-\frac{2GM}{rc^{2}}}

where t0 is the time experienced by the observer and tf is the actual time elapsed. It says that as you move closer and closer to a gravitating object, you experience lesser and lesser time. The same happens near a black hole. It seems that the objects or light is moving slowly. Such a thing you might have noticed in sci-fi movies such as “Interstellar”. If you haven’t watched it go and watch it, they have demonstrated Einstein’s theory beautifully.

2. Precession of Mercury’s orbit

Earlier it was discovered that the orbit of Mercury is slightly different than calculated. It could mean only two things: either there is some other hidden planet beyond Mercury deviating its path or the theory which predicts the Mercury’s orbit must be changed. With Einstein’s theory, the correction was made and the obtained results were very much accurate.

(Image: Lumen Learning)

3. Bending of light

This is one of the most beautiful consequences which you might have seen in almost every book on GR. It says that light gets bent on the curvature of space-time due to a massive object and moves on a geodesic.

Image: UIA (Department of Physics)

Thus the observer can see the light source beyond massive object even when the object obstructs the line of sight.

There are many other consequences such as gravitational waves, gravitational redshift, etc. but covering every one here is not possible in a single post, but they are indeed very interesting to learn. One of the very important consequences of GR is black holes and its studies.

Einstein’s theory of general relativity is one of the most promising theories. Recently there have been many theories popping out, trying to unify this theory with quantum mechanics leading to Quantum Gravity and many other theories. The race to unify all the fundamental theories of physics is on, and soon we might have a Grand Unified Theory which unifies all the theories of physics.

Read other articles related to Science only at thehavok.com

Transparent Solar Panel: Why Is This The Ultimate Game-Changer

Harshil Bhanushali
-
2
Transparent Solar Panel: Why Is This The Ultimate Game-Changer

There was a time when buildings were made of concrete, nowadays glass is used. But shortly skyscrapers will be made of Transparent Solar Panels. Believe it or not, but a team of researchers at MIT achieved a breakthrough in the field of Solar by developing Transparent Solar Cells.

Professor Vladimir and Dr Miles Barr PhD with TLSC
Professor Vladimir Bulović (left) and Dr Miles Barr PhD ’12 (right) with TLSC. (Image: MIT Energy initiative Credits-Justin Knight)

Inventing a new solar technology, to compete with the existing one is a challenge in itself. But a transparent photovoltaic cell (PV) is a Game-changer. “You can deploy it on an existing surface without modifying the look of the underlying material”, says Professor Vladimir Bulović professor of Electrical engineering and MIT’s Microsystems Technological Laboratories.

Trying is Another Way of Innovating

Many other research groups had previously tried to make ‘Pellucid’ solar cells with opaque PV materials. They made it so thin that they appeared translucent. Segmentation is the process of mounting pieces of solar cells on windows with gaps to see out. But these approaches generally entail a barter between Transparency and Efficiency. “When you start with solid PV materials, the more you make the material glassy, the less effective it becomes”, says Miles Barr Ph.D. ’12, president and CTO of Ubiquitous Energies, Inc.

  • Semi-transparent Perovskite cell achieved peak AVT of 77% and 12.7% efficiency.
    [ Source – Science Direct ]
  • Transparent Polymeric Solar cell having active polymer hetero-junction, PBDTT-DPP: PCBM, and Ag nano-wires as the cathode.
    [ Source – Science Direct ]

An Extra-Ordinary Thought

Dr Richard Lunt with prototype of TLSC
Dr Richard Lunt with a prototype of TLSC.

The Transparent Revolution gained momentum when Richard Lunt an MIT postdoc and assistant professor at Michigan State University decided to use the properties of Glass itself. He speculated making a solar cell that would absorb all the light except the part that allows us to see. Light, being electromagnetic radiation gauging a spectrum of wavelengths, each containing energy that can be potentially harvested by a solar cell.

But we can see only a part of the spectrum, so-called visible light. With the right combination of design and material, the light that we detect would be able to pass right through it and we’d never be aware of it.

Putting The Suggestion Into Action

Inspired by Dr. Lunt’s design and using some wit. The team instead of trying to create a transparent PV cell, they used a Transparent Luminescent Solar Concentrator (TLSC). As big as the name sounds the tech is as simple and brilliant. TLSC consists of organic salts that absorb light in UV and near-infrared region(NIR) and luminescence (glow) emitting another wavelength of Infrared light. This light is then guided to the edge of the underlying material (generally glass) where thin strips of conventional PV cells convert it into electricity.

TSC model arrangement
A TSC model allowing visible light to pass through and absorbing UV and NIR light. [ Source- MIT Energy Initiative]

Previous ideas focused on thin active layers with absorption concentrated in the visible region providing a very low efficiency of <1 % or poor average visible-light transmissivity (AVT) of 10-35 %. Since both these factors could not be optimized simultaneously. They created a heterojunction Organic PV cell utilizing a molecular organic donor, chloroaluminium phthalocyanine, and organic acceptor, C60 (Fullerene), the perfect material that works in NIR and UV spectra.

spectral graph showing differences in absorption spectra of TLSC and conventional PV
Spectral Response of Conventional and Transparent PV cell. The critical gap shows that TLSC does not absorb visible light. [ Source- MIT ]

The Setup Of Transparent Luminescent Solar Concentrator

The anode of the cell is coated with Indium-Tin Oxide (ITO), ClAlPc, C60, Bathocuproine (BCP), and MoO3. ITO and MoO3 are the fundamental materials for the transparent electrode, while BCP increases power conversion efficiency by 3% also acting as a buffer layer between Al and C60. The cathode is coated with Ag. The transparent NIR mirror grown separately on quartz called Distributed Bragg Reflector (DBR) was coupled with diffraction gratings.

The role of DBR is to trap the NIR light creating a crystal such that it reflects all the NIR light to prevent leakage from the backside. Diffraction gratings bend the incident light at oblique angles to increase the optical path length. Broadband Anti-reflective coatings are also used to minimize the leakage of light on the backside of panels.

setup of cell contents in order
Assembled TLSC with glass as a substrate with ITO/MoO3 as anode and Ag as cathode.
[ Source- Science Direct]

Although the most special ingredient is NIR fluorescent transparent dyes. These chemically engineered dyes absorb UV and NIR light, emitting visible light. This Marvelous dye is developed from a luminophore blend of canine and cyanine salts.

Change: Coming Soon

The most awaited moment in a researcher’s life is the result of his invention. “Our panel maxed transparency at 86% which was an accomplishment in itself not yet achieved by any other transparent PV cells”, says Dr. Bulović. But success often comes at a price, “Our panel’s efficiency was ver low-around 2%”.

In a detailed theoretical publication, Dr. Lunt and Dr. Bulović and others calculated that their design could reach an efficiency of up to 12% as compared to conventional solar cells. An array of Transparent cells “Stacked” was able to reach an efficiency of 10%. But the team believes that they could reach the limits by carefully configuring PV materials.

Ubiquitous energy states that applications for these panels are almost limitless. And the better part is that the solar windows not only slashes cost but also cut air-conditioning cost since the large part of the light that raises temperature is absorbed. And for the best part, these coatings cost little and are applied at room temperature making them easy to deposit. They could also be retrofitted onto existing glass panels infrastructure at a low cost. Assuming just 5% efficiency and a vertical area footprint of a normal skyscraper, the power generated could fulfill more than a quarter of all the electricity needs of the building.

In 2016 the prototype was launched ( 1 ft * 1 ft) with the highest transparency achieved and an efficiency of 7.6 %. The company entered into a partnership with various glass manufacturers. This company promises Clean Power View technology and we will be looking right through it.

Check out the other posts related to Technology written by our authors at thehavok.com

Dark Energy & the Expanding Universe

Keith Kamson Fernandes
-
11
Dark Energy & the Expanding Universe

It is known to us that the expansion of the Universe is accelerating, rather than slowing down due to gravity. This expansion is said to be caused by Dark Energy, which is said to composes about 68% of the Universe, but even though it is so abundant, its nature is beyond understanding for physicists as of now.

Dark Energy was first observed by examining the light from extremely distant signals like supernovae. When scientists measured the distance and red shift, they concluded that the Universe isn’t made up of matter and radiation only, but also a new form of energy that would change the fate of Our Universe. 

What is Dark Energy?

Dark Energy is an unknown and hypothetical form of energy that affects the Universe by producing a negative gravity or anti-gravity i.e. it acts against gravity. This is being theorized from the observable properties of distant supernovae, which show that the universe is expanding at an accelerating speed. Like Dark Matter, Dark Energy is also not directly observed, but is rather from observations of gravitational interactions between cosmological bodies. 

Possible fates of the Universe due to Dark Energy
Possible fates of the Universe due to Dark Energy (Image: NASA/ESA and A. Riess (STScI))

In 1915, when Albert Einstein gave his world famous paper, General Theory of Relativity, which showed the curvature of space-time on one side to the presence of energy and matter in the Universe on the other side. 

In the paper, he had given in one of his ten field equations,

R-\frac{1}{2}Rg=8\pi GT

where G  is the gravitational constant. Although this is the simplest form of the equations the freedom remains to add a constant term. This “cosmological constant” was what Einstein added in order to achieve a static universe, and it is given the symbol Λ

R-\frac{1}{2}Rg+\Lambda g=8\pi GT

The cosmological constant  given by Einstein was a component that would oppose the gravity in his model and keep the Universe in balance i.e. the Universe would neither expand or contrast but it  applicable to a static universe only. But our Universe isn’t static, this is now considered as the biggest blunder made by Einstein.

These galaxies are selected to measure the expansion rate of the universe, called the Hubble constant. The value is calculated by comparing the galaxies' distances to the apparent rate of recession away from Earth (due to the relativistic effects of expanding space).
These galaxies are selected to measure the expansion rate of the universe, called the Hubble constant. The value is calculated by comparing the galaxies’ distances to the apparent rate of recession away from Earth (due to the relativistic effects of expanding space). (Image: ESA/Hubble)

The Universe is unstable, was proven by Russian physicist Alexander Friedmann in 1922. He found out that the cosmological constant was wrong as the Universe was not static. He assumed that the Universe is full of matter and radiation, and is curved. He also added that the Universe is homogeneous and isotropic i.e. same in all directions and at all locations. To prove these assumptions he gave two equations

(H^{2}-\frac{8}{3}\pi G\rho )R^{2}= -kc^{2}

and   [(\frac{1}{R}\frac{dR}{dt})^{2}-\frac{8}{3}\pi G\rho ]R^{2}= -kc^{2}

Where, H is Hubble constant (which indicates how fast the Universe is expanding), R is scaling parameter and k is curvature parameter ( which indicates the rate of expansion of the Universe and whether or not that the expansion rate is increasing or decreasing. It also indicates the future fate of the universe.). The curvature parameter indicates whether the universe is open or closed. The above equations do not specify the nature of the density ρ.

These equations show that the Universe either contracts or expands depending on the content and rate of expansion of the Universe, which shows that it evolves with time. Thus this proved that the Universe wasn’t static but rather unstable.

Studied lensed quasars of H0LiCOW collaboration: Using these objects astronomers were able to make an independent measurement of the Hubble constant. They calculated that the Universe is actually expanding faster than expected based on our cosmological model.
Studied lensed quasars of H0LiCOW collaboration: Using these objects astronomers were able to make an independent measurement of the Hubble constant. They calculated that the Universe is actually expanding faster than expected based on our cosmological model. (Image: ESA/Hubble)

The Universe is expanding, was proven by Edwin Hubble in the late 1920s. He observed that the redshift of galaxies is directly proportional to the distance of the galaxy from the observer i.e. Earth when he was studying the galaxies outside the Milky Way. This gave birth to the Hubble Law, which is now called Hubble-LeMaitre Law, which states that:

Objects observed in space with more than 10 mega parsecs (Mpc) (1 parsecs or 1 pc = 3.26156 lightyears) are found to have a redshift, interpreted as a relative velocity away from Earth;

This Doppler shift-measured velocity of various galaxies receding from the Earth is approximately proportional to their distance from the Earth for galaxies up to a few hundred mega parsecs away.

The equation is given as,

ν=Hr

Where, ν is recessional velocity (which is the rate at which an extragalactic astronomical object recedes from an observer as a result of the expansion of the universe), H is Hubble constant and r is distance.

The value of Hubble constant has varied over the years. The current value of  H is 73.8 km/s per Mpc.

These two finding proved that Einstein’s cosmological constant was not applicable to our Universe. The findings were later acknowledged by Einstein himself, who considered this as a blunder. 

Theories Related to Dark Energy

Cosmological Constant (Λ)

In this theory, Einstein’s blunder is said to be perfectly suitable for Dark Energy and that it is the intrinsic and fundamental energy of space. Since mass and energy are related then according to the famous equation given by Einstein that E=mc2, then his theory of general relativity predicts that this energy will have a gravitational effect. This is usually called vacuum energy as it is the energy density of an empty vacuum.

The cosmological constant has a negative pressure which is seen through classical thermodynamics, this negative pressure is equal and opposite to its energy density so due to this it causes the acceleration of the expansion of the universe. The current cosmological model i.e. the Lambda-CDM model (or the current cosmological model) includes the cosmological constant as an important feature and also the cosmological constant is the only solution for the accelerated rate of expansion of the Universe. 

Quintessence

In this theory of Quintessence, the observed acceleration of the scalar factor is caused due to the potential energy of the dynamical field called the Quintessence field. This differs from the cosmological constant as it can vary with space and time. So that this doesn’t clump and form a structure like matter, the field has to be very light so that it has a very large Compton Wavelength which is equal to the wavelength of a photon whose energy is same as the mass of that particle i.e. E=hmc where his the Planck’s constant, m is mass of the particle and c is the speed of light.

Dark Matter and Dark Energy Interaction

In this theory, it is believed that dark matter and dark energy are both a single phenomenon that modifies gravity at various scales.

How will Dark Energy affect us?

Dark Energy is said to lead the Universe to any one of these three scenarios:

Closed Universe

In this theory, it is believed that the Universe will expand upto a certain point and stop due to gravity, but then start to contract till it reaches a point that all matter is collapsed, this is also called the Big Crunch. 

Open Universe

In this theory, it is said that the universe will continue expanding at an accelerating speed. But later on, the acceleration caused by dark energy will be so strong that it overcomes the effect of gravitational, electromagnetic and strong binding force which will make the Universe to destabilize and lead it to explode. This is also called the Big Freeze or Big Rip.

Flat Universe

In this theory, the expansion of the Universe will continue and will remain stable. But it is also believed to end up like the Open Universe

Fate of the Expanding Universe
Fate of the Expanding Universe (Image: SkyServer)

COVID-19 Breakthrough: Innovative Masks that can kill Corona Virus pathogens

Om Desai
-
5
COVID-19 Breakthrough: Innovative Masks that can kill Corona Virus pathogens

SARS-CoV-2 or COVID-19 or corona virus, has put the whole world in danger. It has risked lives of millions of people all over the globe. Everyday lakhs of corona virus cases are reported around the world. Researchers are trying their best to develop vaccines and better ways to prevent its spread. At the same time common people are trying to avoid it in best ways they can. Paper masks are made mandatory so that air-borne spread of the disease can be prevented as a part of these attempts. But, with their widespread use, they also have certain drawbacks. Biggest of which is disposability and efficiency to safeguard mankind against corona virus.

To overcome this highly contagious and rapidly spreading corona virus, researchers at EPFL Laboratories, Switzerland has come up with a revolutionary solution. They have fabricated materials that can be used in personal protective masks, which can inactivate airborne pathogenic substances. Along with this, it can also offer reusability to its users.

Basically, they have made a sort of “filter paper” from Titanium-Oxide (TiO2) which can trap pathogens when exposed to UV-light. This newest development can be used in personal protective equipment kits (PPE), ventilation systems and in air-conditioning systems. The masks which currently available rely on layers of non-woven polypropylene plastic microfibers. These are not environment friendly and cannot trap pathogens efficiently.

But, with titanium oxide nano-wires, antibacterial and antiviral properties can be achieved. Titanium oxide has ability to speed up the reactions as a catalyst with combination of light. This is known as photo-catalytic property. Also, this material has high water absorbing abilities which help in eliminating the pathogens.

How it works fighting Corona Virus?

It easily absorbs water on its surface because of super-hydrophilicity property.

With better absorbing ability, it can trap moisture exceptionally well and droplets of viruses and bacteria with that.

This trapped moisture along with UV- light exposure helps to form ROS-reactive oxygen species, like hydroxyl radicals (OH.), hydroperoxyl radicals (HO2.), hydrogen peroxide (H2O2), singlet oxygen (1O2) and superoxide radicals (O2-.).

This favors formation of oxidizing agents or reactive oxygen species (ROS), like hydrogen peroxide, when exposed to ultraviolet radiation.

They are capable of destroying corona virus pathogens immediately as well as others on the surface which are inactivated previously photo-catalytically.

explaining elimination of COVID-19 pathogens

Researchers used commercial DNA to know how ROS-reactive oxygen species operate, to determine the rupturing of DNA-strands in very local area. This was observed with the help of AFM technology, which is Atomic force Microscopy. It showed that, with increasing time of incident UV-light, there was decrease in DNA-strands and eventually only debris were left. As seen in figure. b, there is eventual breaking of DNA molecules in presence of UV-light. Thus, it depicted the elimination of bacterial bodies from the sample. 

Corona virus Mask prototypes

Figure a. Mask prototype attached to 3-D printed frame which can be used for general purposes and PPE- kits to fight against corona virus.

Figure b. disinfecting of prototype mask under UV-light and clearing the surface from germs and pathogens.

Figure c. prototype mask in actual conditions.

Advantages and Benefits against fighting Corona virus:

  • easily sterilizable and reusable mask

  • antiviral and anti-bacterial to fight COVID-19

  • Can be reused more than 1000 times, which is far better than ordinary masks that are being currently used to fight against corona virus.

  • Overcomes environmental and public health issues created by disposal of ordinary masks.

  • Can also be installed in ACs and ventilation systems to have protection against air-borne nature of disease.

  • Easy to handle and wearable, and can be added to personal protective kit for COVID-19 health workers and also ca be opted for regular use by common people.

Present and future of this technology:

The prototype of this mask has already been made (which was shown earlier in the figure). Also, large scale production of the masks is possible. While only using laboratory equipment and facilities, it is possible to manufacture them. They alone can produce 200 m2 of filter paper in a week, which is quite incredible. This can fulfill demand of 80,000 masks per month to fight against corona virus.

During their production, these titanite nano-wires are often oxidized at high temperatures to remove volatile impurities. This safeguard users from inhaling the nano-particles that are used to manufacture them and makes it chemically stable.

A start-up, Swoxid, approves that these nanowires can also be used in air-conditioning and ventilation systems. This fact increases their usability apart from COVID-19 mask preparation. Following this, they have already prepared this technology to move out of the lab.

Thus,
No matter how big this mortal disease be, we, as humankind, always will overcome and leap forth to pursue our goals. 

Creating The Most Precious Liquid From Air

Harshil Bhanushali
-
0
Creating The Most Precious Liquid From Air

Sustainable Development! Well most of you have heard about this term once in your life. But the major breakthroughs in Science turning this Utopian idea into reality are often unheard of. Let’s dive into the field of Path-Breaking and Efficient Innovations changing the world.

Creating The Most Precious Liquid From Air

Magic is all deception, producing a coin from nothingness, flowers from thin air or water from empty space? Did I just say water, well that’s not a deception that’s Science! A team from Researchers from IIT Madras have developed a new machine called AWG (Atmospheric Water Generators). The team started in 2016 as a part of “Water for Future”, an initiative by IIT Madras called VayuJal.

Vayujal Technologies on the precious liquid, water
Vayujal Technologies (Image: Facebook/Vayujal)

The Machine circulates Ambient air (humid air) through the duct where air is filtered, then into the condensation chamber where it is cooled to Dew Point. The water vapor collected is then condensed and water is passed through 8-stage filtration process and minerals are added. The End product is Mineral Water from Air! Amazing, Right!

Working of AWG
Working of AWG (Image: Vayujal)

Further more Co-Founder and CEO Ramesh Kumar says that the design on cactus plant inspired the condensation surface, which was designed nano-structurally to provide more surface area and efficiency.

Today Vayujal has been able to produce mineral water at a rate of ₹1.8-2.0/liter. And they are planning to cut the cost by 5 times! The output still depends on climate conditions and areas with high relative humidity has a plus point, that is why they are developing an algorithm to maximize output.

After speaking with Prof. T. Pradeep ( Co-Founder and Director of VayuJal) about these problems, I asked “What if we keep them near the places where we hang clothes?” to which he replied (laughing) “Well that thought never crossed our mind! But if u have 100-120 clothes hanging at a time then you can keep it there. The machine needs ventilation just as we do, so I don’t think balcony is your option!”. After this he added, “We have made Vayujal fully functional with added Solar panels so that it can sustain itself and provide water at a reasonable cost!”

Now this is an idea out of the Box or shall I say ‘Thin-Air’.   

Innovation is the unrelenting drive to break the status quo and develop anew where few have dared to go.

Steven Jeffes

Check out the other posts related to Science written by our authors at thehavok.com

LHC – “BIG BANG MACHINE” – The Crown Jewel Of CERN

Adithya A Rao
-
10
LHC – “BIG BANG MACHINE” – The Crown Jewel Of CERN

The Large Hadron Collider is the most beautiful and the most sophisticated machine mankind has ever built. Despite the underlying principle being simple, the LHC has been a very complicated machine to perform experiments on. But all the painstaking process has not gone in vain, and it has proven to be the saviour by confirming the predictions of many theories, hence being a milestone in modern physics.

LHC collider tunnel
The collider tunnel at Large Hadron Collider [Image: Lancaster University]

History of elementary particle physics

At the end of the 19th century, physicists believed that physics was completed and there was no new theory needed and things were finally declining. But poor them, they had no idea what nature had in store for them. In a short span of just 50-60 years, things had drastically changed. Now they were sitting there staring at the mess in front of them. There ware so many particles discovered that it was all bizarre and unexplainable. They were all such unexpected discoveries that upon the discovery of the muon, Nobel laureate Isidor Isaac Rabi famously quipped, “Who ordered that?”. Physics was like chemistry before Mendeleev gave his periodic table, in complete chaos, helpless about the zoo of particles mocking at them. 

Willis Lamb began his Nobel Prize acceptance speech in 1955 with the words,
“When the Nobel Prizes were first awarded in 1901, physicists knew something of just two objects which are now called ‘elementary particles’: the electron and the proton. A deluge of other ‘elementary’ particles appeared after 1930; neutron, neutrino, µmeson, πmeson, heavier mesons, and various hyperons. I have heard it said that “the finder of a new elementary particle used to be rewarded by a Nobel Prize, but such a discovery now ought to be punished by a $10,000 fine”.
[Source: Les Prix Nobel 1955, The Nobel Foundation, Stockholm.]

This was all sorted by Murray Gell-Mann who gave the most elegant way of quantifying these elementary particles. It is based on the SU(3) model of group theory and is called the eightfold way. He managed to triumphantly explain the classification of all these particles. But he did not stop there, he also predicted the existence of new particles based on his theory.

Detection of the elementary particles

The discovery of most of these elementary particles was all thanks to cosmic rays. 
‘Cosmic rays’ is the godly name given to the stream of particles from outer space entering the Earth’s atmosphere. It comprises of mainly high energy protons, electrons and other atomic nuclei,  darting at near-light speeds. These high energy particles rain down on Earth, smash head-on with atoms in the upper atmosphere and tear them apart. Thus they form a shower of ‘secondary particles’ which then reach down to the Earth. These particles can be detected in laboratories by using bubble chambers where the paths followed by the particles is registered. This path can be then analyzed and used to determine the nature of the particles. But most heavy particles are unstable and hence decay into lighter particles before reaching down. And this means only light particles can be detected in laboratories. Thus cosmic rays can never be a possibility to confirm the existence of these heavy particles. This means that the confirmation of predictions of elementary particle physics could not be done using them. Physicist needed a new method to recreate this natural phenomenon in laboratories.

Neutrino in a hydrogen bubble chamber
The invisible neutrino strikes a proton where three-particle tracks originate (lower right). The neutrino turns into a mu-meson, the long centre track (extending up and left). The short track is the proton. The third track (extending down and left) is a pi-meson created by the collision
[Image: Argonne National Laboratory]

What does Large Hadron Collider do?

Particle accelerators are old science and have already been set up in lots of places. The Large Hadron Collider, set up by CERN  is the most advanced and the costliest particle accelerator built till date and it lives up to the expectations.

Charged particles are deflected by electric and magnetic fields. The particle accelerators take advantage of this phenomenon to accelerate the particles, guiding them through the huge, circular tunnels. Superconducting magnets at temperatures close to absolute zero (-273.15 ℃), cooled using liquid helium, are used to guide these particles. They form beams travelling at phenomenal speeds, which upon completion of few rotations gain a colossal amount of energy and momentum. These guided beams then collide head-on expending all the gained energy into creating new particles. CERN has, till date, collected petabytes of data, running the experiment numerous times and generating datasets of the statistical data obtained.  

LHC has been called ‘The Big Bang Machine’ in contemporary literature. This is because it was used to recreate the conditions of the universe shortly after the Big Bang. On the 7th of November 2010, LHC collided two beams of lead ions instead of protons to recreate a mini Big Bang. The temperatures being reached up to a million times hotter than at the centre of the Sun. 
Another great and publicly celebrated discovery is that of the ‘God particle’, the Higgs Boson. It is the particle corresponding to the Higgs field, which gives mass to all other particles. On July 4 2012, scientists at CERN declared an end to the long-lasting search for the God particle, which was observed in a high energy proton-proton collision.
Further experiments are being performed in LHC hoping to find out more about the dark matter which physicist conjecture, is made up of particle we haven’t theorized or detected yet. 

In contemporary literature

Large Hadron Collider has been, in contemporary literature, called ‘The Doomsday collider’. This is because there have been many conspiracy theories about LHC ending up destroying the world. It may be about creating a black hole, or about Higgs Boson causing a quantum fluctuation called vacuum bubble that sends the universe into instability and finally destruction, or about strange matter being created that ends up converting ordinary matter into strange too, and whatsoever. But scientists have been dismissing all these possibilities from ever since. CERN has hosted a page on its website regarding the safety of its collider, you can view the page here.

Image for representation purpose only. [Image: infographicsmania]

Right now the LHC has entered a Long Shutdown 2 (LS2). The first shutdown LS1 in 2013 was to increase the energy of collider from 7 TeV to 13TeV. This time it is for a few major upgrades in the upper limit of the energy of the collider. In this time scientists probe loads of data gathered during the running period, keeping the search and curiosity of physics alive. The LHC has lived up to its fame of being the most complicated device ever built by playing a pivotal role in making discoveries which otherwise would never be possible.

Flow Chemistry and Reactive Extrusion- Newer And Better Chemistry

Om Desai
-
1
Flow Chemistry and Reactive Extrusion- Newer And Better Chemistry

Introduction to Flow Chemistry:

As the name suggests, rather than in classical batch approach, here in chemical reactions are run in continuously flowing streams . Using flow chemistry, eventually the risk of working in the hazardous environment for chemists can be minimized and yield of the reaction can also be increased at the same time. It mainly works on the concept of pumping the reacting materials and required catalysts using many reactor types to perform the reactions. It is mainly used where the starting material is limited and small-scale reactions are preferred.

Basic difference of Flow Chemistry from batch method:

  Flow Chemistry Batch method
Stoichiometry Flow rate and molarity are
used to set stoichiometry		 Molar ratio of reagent is
used to set stoichiometry
Reaction Time Determined by Residence Time
i.e. amount of time reagents spend
in reactor zone		 Determined by the time a
vessel is stirred under fixed
conditions.
Flow Rate Controlled by reagent exposure
time under specified conditions.		 Controlled by flow rates of
reagent streams
Mixing and
Mass Transfer		 It is easy, as its diffusion within
very small regions of reagents		 Relatively Harder
Temperature Control
and Heat Transfer 		Attained easily, as high
surface area to volume ratio		 Relatively Harder

Examples of Flow Chemistry:

Oxidation of a primary alcohol

oxidation of primary alcohol
oxidation of primary alcohols give aldehydes in this case. Click here

Williamson Ether Synthesis

williamson ether synthesis
in Williamson synthesis, alcohol here gives ether as a product. Click here.
  • Recent examples also include the flow synthesis of ciprofloxacin, an essential antibiotic, and an automated flow system developed by Pfizer, capable of analyzing up to 1500 reaction conditions a day, speeding up the discovery of optimal synthetic routes for both new and existing drugs.
  • Pharmaceuticals
  • Green chemistry
  • Polymer chemistry
  • Catalytic reactions

Advantages over Batch Method:

  • Because of the inherent design of continuous flow technology, it is now been possible to get products of high quality, with less impurities and a faster reaction cycle to produce them.
  • Also, as the conditions of the reactions can be modified as required, it provides a wide range of product possibilities and better yielding conditions than the batch method.
  • Flow chemistry safeguards the handling of reactants which are of human health hazards and thus increases the feasibility of the reactions.
flow chemistry vs batch method
heat out under batch methods and flow chemistry techniques. Click here.

Thus, here it can easily be observed that with the use of flow chemistry techniques over batch methods, higher temperatures are required for the synthesis via batch methods whilst they are lower by 400C in case of flow chemistry techniques.

Disadvantages:

There are certain disadvantages of flow chemistry, although it is still considered best way to proceed reactions.

  • Heterogeneous mixtures are a bit difficult to process.
  • sometimes there can be clogging in reaction tubing, which can create problems.
  • If the chemical reaction is slow, there is no such major advantage over batch method.
  • Also there are certain issues regarding scaling up of technology for commercialization.

Reactive Extrusion:

Along with this, to make the concept of flow chemistry more environment friendly and more feasible, this is a technique which makes the chemical reactions to happen completely solvent free. This process includes usage of continuous extruder-reactor, with exceptional mixing capabilities at molecular level.

As the reactor like this can be derived from the conventional plastic extrusion machines, it makes the processes simpler. Moreover, this process is more secure, as it is confined and realized in low reaction volumes.

Because of this, Reactive extrusion requires less capital investment and offers good environmental performance with lower energy consumption compared with processes equipped with batch reactors. Simultaneously, Reactive systems are also more compact and therefore require less space.

This process also creates some engineering challenges, as industries have to completely redesign the equipment and work space. Nevertheless, polymer and material experts are widely using the technique, and this is indeed the future of green chemistry and in turn, creating a new advancement in the modern technologies.

Thus, with the increasing industrial needs for better products and faster outputs with more sustainable processes, flow chemistry and reactive extrusion have proved to be helpful and reliable and at the same time more cheaper, cleaner, safer and faster products are obtained.

reactive extrusion

Newest Advancement In technological Sector:

Asia Flow Chemistry System, developed by SYRRIS, is most recent and most advanced flow chemistry product range. This can perform numerous tasks, impossible with Batch method, in more simpler and better way. With this development, Flow chemistry can now be applied to more wider and varied range of synthesis and simultaneously giving precise control to the reaction. Other then these, it can monitor reactions on-line and give continuous analyses, so that reactions can be modified without interrupting its functioning.

Other such equipments, include different types of micro-reactors which can perform various tasks continuously and actively. These tasks include, performing at high pressures, at higher temperatures, with higher Heat transfer capacities, with faster mixing capabilities and many such things that batch method reactors and pumps were not able to provide.

Talking about pumps used in Flow Chemistry, breakthrough was achieved by Vapourtec, with its V-3 pump. This has enabled the creation of the new E-Series flow chemistry system. With its Strong designs and yet easy to use technique, can pump Strong Acids, gases, suspensions and organometallic reagents. Along-with this, it provides high advanced control for smooth outputs even at high pressures

Future and Scope:

Although it seems that Flow chemistry is almost complete and fully developed, their are many aspects which are still under R&D phase. For instance, still companies and industries are trying to manage more effective and efficient ways to pump the fluids and also to reuse them or dispose them properly after their use. Some Advancement can also be expected in the Micro-reactors and to develop other materials used to manufacture them.

Below are insights, which clearly show that market for Flow Chemistry is emerging and can opt a major growth in the next decades.

flow chemistry insights
Market size of Flow Chemistry crossed USD 1 billion in 2018 and will witness a CAGR of approximately 11 % between 2019 and 2026. Click here.

With changing scenario of industrial chemistry, these techniques can be robust, time saving and cost efficient all at the same time.

—OSD

Special Relativity

Vibhor Singh
-
6
Special Relativity

The principle of relativity stated that the laws of physics are invariant in frames moving relative to each other with constant velocity. The relation between positions in two frames of reference was given by the Galilean transformations. But when physicists found out that Maxwell’s laws of electromagnetism were not invariant under Galilean transformations, the physics world was in chaos. There were only two possibilities. Either Maxwell’s theory which gave promising results was wrong, or the Galilean transformation was not the right one and it needed a correction.

In 1905, Einstein came up with the special theory of relativity. He inculcated the transformation equations mathematically developed by Lorentz, rather than the Galilean transformation and showed that this was, in fact, consistent with Maxwell’s theory. This theory was a revolution in physics and it changed most of the physics we know today.

Einstein proposed the universe was not the intuitional 3-D space but is actually 4-D. Instead of treating time as a parameter, Einstein treated time as a dimension winded with the other 3 spacial dimensions, making space-time 4 dimensional.

Here we will use the top-down approach rather than the bottom-up approach to get ourselves into the special relativity. We will think of time just like space except for the fact that we can move only forwards in time. Another thing to bear in mind is that no object can go faster than the speed of light, 299,792,458 m/s.

In Newtonian mechanics, we think of the whole of the space at a given instance of time. But this approach is completely flawed. The division of space-time to space and time is not specified by nature but is something made up by us. All the paradoxes regarding the special theory of relativity will disappear if we think about space-time universally. In special relativity, time is not universal, it is different for observers moving relative to each other with different speeds. In 3-Dimensional Euclidean Space, the shortest distance between two points is a straight line. But in a 4-Dimensional space-time, straight line corresponds to the longest interval (we can call this interval the elapsed time), this being the result of the fact that the more you move in space, the less you experience time. More specifically, the rule of thumb is that “on a curly line, you always experience less time”. The formula for obtaining the elapsed time interval is given by \tau ^{2}= t^{2}-\frac{x^{2}}{c^{2}}

In this diagram, the particle which takes the curved trajectory “experiences” lesser time because it will be moving more in space - relativity
In this diagram, the particle which takes the curved trajectory “experiences” lesser time because it will be moving more in space

There is a famous paradox (not actually a paradox, so let’s call it a pseudo-paradox) called the twin paradox. Suppose there are twin siblings Alice and Bob. They synchronise their clocks, then Bob sets on a journey to a distant star, say Alpha Centauri, in a rocket with constant velocity and then comes back to Earth. Alice has aged more than Bob. This is because Bob has travelled more distance in space, i.e he has taken the curvier path, while Alice has stayed in the same place.

But, from the equivalence principle, there should be no experiment that can show who is stationary and who is moving. Thus for Bob, Alice should be moving and hence she should be aged less than Bob. So is the equivalence principle violated? If we look closely, the principle is not violated, because Bob has to accelerate to return to Earth. So truly speaking, his frame of reference is not inertial.

The paradox says that by the virtue of symmetry, according to the reference frame of Bob, Alice has moved away and come back, so it poses a question as to why Bob has aged lesser than Alice and not vice versa. The reason this happens is that they both travelled different “space-time” distance. So, we have seen that if we talk in terms of space-time, “there are not any actual paradoxes”. It is just because we are not ‘used-to’ with high velocities. We are just not familiar with objects moving with velocities compared to that of light.

So was Newton wrong? No, he was not actually…

For now, consider the speed of light to be 1, thus the distance travelled by light is the same as time elapsed,  x = t.

In two dimensions (1 space and 1 time), the path followed by light forms a straight line

In three dimensions (2 space and 1 time), this is replaced by a cone, called the light cone.
In three dimensions (2 space and 1 time), this is replaced by a cone, called the light cone.

The upper half of this cone is called the future light cone, and the lower half is called the past light cone. Any massive body always moves in a trajectory which is always inside the light cone.

(Image:Wikipedia)

The region outside this cone is called spacelike, no massive particle can reach this region. The region inside the cone is called timelike, with all massive particles taking timelike trajectories. The cone x = t is called “lightlike” or “null” trajectories. This is the path taken by light (photons).

So why hadn’t Newton noticed such a thing? This is because the speed of light is very huge. If we draw the cone in standard units of one meter and one second, it would look like,

There is a very thin separation between x = t and t = 0, which is kind of similar to Newton’s thinking which is
There is a very thin separation between x = t and t = 0, which is kind of similar to Newton’s thinking which is
relativity

So Newton was not wrong, but he did not consider the finiteness of the speed of light. All of Newtonian mechanics can be obtained as a limit of relativistic mechanics, the limit v<<c.

Einstein did not stop here. He was puzzled by Newton’s gravity and the possibility of sending gravitational signals instantaneously. So he went on further to give the relativistic theory of gravity, the general theory of relativity (GR). In GR, spacetime is not flat but curved, and gravity is nothing but the manifestation of curvature of spacetime.

Flexible Electronics: Next Ubiquitous Technology

Umakant Bohara
-
8
Flexible Electronics: Next Ubiquitous Technology
A flexible electronic circuit made with the new liquid metal tracks.
image source

Electronics is one of the many fields which has been witnessing large scale evolutions. This field was once known for its heavy, bulky and rigid devices, which are now replaced with lightweight, soft and flexible appliances. Flexible electronics is an emerging and revolutionary technology having the potential to upgrade conventional electronics and avail ease of recycling, low-cost, flexibility, lightweight, and easy to use.

Deposition Method

The mainly used deposition techniques to develop flexible devices are Screen printing, Ink-Jet printing, Photolithography, Soft Lithography, Doctor blading, Spin coating, etc. The roll to roll process is used to fabricate such devices for large area and low cost.

Applications

It has applications in various societal sectors:

  • including healthcare
  • the automotive industry
  • human-machine interfaces
  • mobile communications and computing platforms
  • embedded systems in both living and hostile environments

Market-specific applications, such as human-machine interactivity, energy storage, and generation, mobile communications, and networking.

 To enable all these applications, electronic devices need to be flexible, lightweight, transparent, stretchable, and even biodegradable. They can fulfill these requirements and are thus becoming increasingly important to next-generation electronic device platforms.

Flexible Electronics: Present and Future

flexible electronics
image source

Silicon technology has led the way towards miniaturizing devices, increasing cost-effectiveness, and improving its performance. But the material rigidity of silicon poses a threat to the ubiquitous use in soft electronics (flexible and stretchable electronics) applications. As a result, the research community is in an extensive search of prospective material that has the potential to overcome the drawback of rigidity.

flexible electronics

Carbon nanotubes (CNTs) and graphene prove to be useful for such applications. These materials overshadow silicon in areas of elastic properties, electronic, optoelectronic, and thermal properties. The discovery of nano-carbon materials has created a scope for advancements in soft electronics and has set a trend in the technical world.

Transition-metal dichalcogenide (TMD) materials and boron nitrides are non-Carbon graphene-like 2D materials that have also gained significance in the field of soft electronics.

These materials are deployed in countless applications, but still, there are a few limitations due to the lack of high yield assembly processes. The orientation of CNTs has to be in a specific direction along with desired density and chirality. Large-area manufacture of graphene is achievable, but the damage during the transfer to a substrate hamper the device performance. Hence, finding efficient techniques for assembling CNTs and transferring graphene is one of the hot topics in the research domain.

In the coming future, we expect the industry to witness a fusion of wearable technology with flexible electronics. The progress in the field of Organic sensors would contribute to the commercial availability of features like gesture recognition, contactless control, and biometric sensor arrays.

Stretchable silicon will be a broad topic of research as nano-carbon materials will be unable to match the speed of silicon. The existing LED, LCD technology might affect the growth of flexible electronics, still, the foundation for a new era of electronics has been laid, and this Ubiquitous technology would be here to stay.

To read more about such amazing technology and advancements in electronics. Click Here.

Dark Matter: The Invisible Force

Keith Kamson Fernandes
-
13
Dark Matter: The Invisible Force

We know that galaxies in the Universe are kept together with the help of gravity, but the galaxies rotate at speeds that gravity wouldn’t be able to hold them together and would have torn themselves apart. This also applies to galaxy clusters, which has led scientists to believe that something invisible is keeping these galaxies together. Scientists think that this invisible matter is giving galaxies extra mass which would lead to extra gravity that will help in keeping the galaxy together. This invisible matter is none other than “Dark Matter”. Dark matter is currently one of the biggest mysteries in the universe that scientists have been trying to solve for quite some time.

What is Dark Matter?

Dark Matter is a non-luminous matter which doesn’t absorb, emit and scatter light of any wavelength (so basically its invisible) and does not interact with electromagnetic force. It also interacts primarily via the gravity with visible matter like stars, planets, etc.

This collage shows NASA/ESA Hubble Space Telescope images of six different galaxy clusters. The clusters were observed in a study of how dark matter in clusters of galaxies behaves when the clusters collide.
This collage shows NASA/ESA Hubble Space Telescope images of six different galaxy clusters. The clusters were observed in a study of how dark matter in clusters of galaxies behaves when the clusters collide. 72 large cluster collisions were studied in total. (Image: ESA/Hubble)

The matter we see around us like planets, stars, etc. makes up only 5% of the Universe, while dark matter makes up 27% of the Universe and the remaining by another mysterious substance called Dark Energy. The only things related to dark matter is that it’s invisible, exerts a gravitational pull that helps bind together galaxies and distorts the appearance of space.

When did we come to know the Existence of Dark Matter?

The existence of dark matter was discovered in 1937 by Swiss-American Astrophysicist Fritz Zwicky, who taught at the California Institute of Technology. He studied the movement of individual galaxies within the Coma Cluster which is an isolated and richly populated ensemble of over 1000 galaxies about 330 million light years from Earth and located in the constellation of Coma Berenices.  He noticed the huge scatter in the apparent velocities of 8 galaxies with differences more than 2000 km/s. Zwicky applied the virial theorem to the cluster in order to estimate it’s mass.

Coma Cluster that was studied by Fritz Zwicky
Coma Cluster that was studied by Fritz Zwicky (Image: ESA/Hubble)

The Virial Theorem is given by \sum _{i}=\frac{1}{2}m_{i}v{_{i}}^{2}= -\frac{1}{2}\sum _{i}r_{i}\cdot F_{i}

Zwicky estimated the total mass of the Coma Cluster to be the product of the no. of observed galaxies as 800 and the average mass of a galaxy to be 1 billion solar masses. He then took an estimate for the physical size of the system, which he had taken to be about 1 million light-years, in order to determine the potential energy of the system. From there, he calculated the average kinetic energy and velocity dispersion.

He found out that the velocity dispersion for the 800 galaxies with 1 billion solar masses in a sphere of 1 million light-years is 80 km/s. In reality, the observed average velocity dispersion along the line-of-sight was approximately 1000 km/s. Zwicky also inferred an enormous mass for the Coma Cluster since larger gravitational forces induce higher velocities in the objects they attract. He concluded that:

“If this would be confirmed, we would get the surprising result that dark matter is present in much greater amounts than luminous matter.”

And even though the Coma Cluster ranks among the largest and most massive clusters in the universe, it does not contain enough visible galaxies to account for the observed speeds Zwicky measured.

The observations seen by Fritz Zwicky was later confirmed in the late 1970s by American astronomer Vera Rubin who was studying the galactic rotation curve of the Andromeda Galaxy, galactic rotation curve is a plot between the orbital speed of the visible stars or gases in the galaxy and their radial distance from the galaxy’s center. She observed that the stuff at the edges of the Andromeda Galaxy was moving as fast as the stuff moving near the center, which basically violates Newton’s Laws of Motion. It took two years for Rubin to get an explanation for this strange behavior which now holds as the first known evidence of dark matter.

Candidates for Dark Matter

1. Neutrinos

At first, Neutrinos were considered the perfect candidates for dark matter as they barely interact with matter and they don’t absorb or emit light which means that they won’t be able to be detected by telescopes. They also interact with weak force. And unlike other particles, neutrinos are stable, long lived and don’t experience electromagnetic or strong interactions.It is also possible that neutrinos have a non-zero mass, unlike photons which are mass-less. If they are to have the right value of mass based on the total number of neutrinos (and anti-neutrinos) that exist, then it is possible that they could account for 100% of dark matter.

2. Supersymmetry

Supersymmetry is an unproven yet true relationship between two basic classes of elementary classes: Bosons and Fermions. Supersymmetry requires that for every Boson, a Fermion must exist for the same quantum number and vice-versa. It therefore predicts the existence of several new non-strongly interacting and electrically neutral particles which include the super partners of Neutrinos, Photon, Higgs Boson, Z Boson and Graviton. If these super partners were stable then could be cosmologically abundant and help us get a better understanding of the evolution and history of the Universe.  

3. Axions

Axion is a hypothetical elementary particle and a candidate for cold dark matter (will talk about it later in the article). It satisfies the two necessary conditions for cold dark matter:

  1. Non-relativistic population of axions could be present in the universe in quantities sufficient to provide the require energy density for dark matter.
  2. They have only significant long-range interactions which is gravitational

4. Weakly Interacting Massive Particles (WIMPS)

Weakly Interacting Massive Particles (WIMPS) are new hypothetical particles which are said to interact through gravity and other forces. It is also as weak as or weaker than the weak nuclear forces and is non-vanishing in strength. Even though the particle is hypothetical in nature, it is believed that it would resolve a number of cosmological and astrophysical problems related to dark matter.

Classification of Dark Matter

1. Cold Dark Matter (CDM)

Cold Dark Matter is a type of dark matter that moves slowly as compared to the speed of light. It is said to have been present in the universe since the very beginning and has most likely influenced the growth and evolutions of galaxies as well as the formation of first stars. It is said to have the following properties:

  1. Lacks the interaction with electromagnetic force. This is quite obvious as dark matter is dark. Therefore it doesn’t interact with, radiate or reflect any type of energy in the electromagnetic spectrum.
  2. It interacts with gravitational fields. There has been proof of this as astronomers have noticed that dark matter accumulation in the galaxy cluster has a gravitational influence on light from more distant objects that are passing by. This is called gravitational lensing.
Quasars' Multiple Images Shed Light on Tiny Cold Dark Matter Clumps taken by Hubble Space Telescope in January 2020
Quasars’ Multiple Images Shed Light on Tiny Cold Dark Matter Clumps taken by Hubble Space Telescope in January 2020 (Image: ESA/Hubble)

The CDM is said to be composed of Axions and thermally produced WIMPs.

2. Hot Dark Matter (HDM)

Hot Dark Matter is a type of dark matter that moves at ultra-relativistic speed when compared to the speed of light. The distribution of HDM could help us understand the formation of clusters and superclusters after the Big Bang. The HDM is said to be composed of Neutrinos.

3. Warm Dark Matter (WDM)

Warm Dark Matter is a type of dark matter that has properties intermediate between CDM and HDM. The most common WDM candidates are neutrinos and gravitons. The non-thermally produced WIMPs can also be considered as a candidate for WDM.

Proof of Dark Matter

1. Gravitational Lensing

A gravitational lensing occurs when a gravitational field is created by a large amount of matter, like a galaxy cluster, that distorts and magnifies the light coming from distant galaxies that are behind the cluster but are in the same line of sight.

Illustration of Strong Gravitational Lensing
Illustration of Strong Gravitational Lensing (Image: Hubble Site)

By measuring the distortion geometry, the mass of the cluster can be obtained. In cases that were observed, it was seen that the mass-light ratio obtained corresponded to the measurement of dark matter in clusters.

2. Galaxy Rotation Curves

The arms of a spiral galaxy rotate around its galactic center. The luminous mass density of a spiral galaxy decreases as we go from the center to the ends. From Kepler’s Second Law, it is expected that the rotational velocities will decrease as we move away from the center similar to the Solar System, but instead the galaxy rotation curve remains flat or constant as we move away from the center.

Rotation curve of a typical spiral galaxy: predicted (A) and observed (B)
Rotation curve of a typical spiral galaxy: predicted (A) and observed (B)

If Kepler’s laws are correct, then the only way to solve this problem is to conclude that the distribution of mass in spiral galaxies are not similar to the Solar System. Which means that there is a large amount of non-luminous matter/dark matter at the ends of the galaxy.

3. Galaxy Cluster

Galaxy clusters help in finding the existence of dark matter since their masses can be calculated in three different ways:

  1. Scatter of radial velocities of the galaxies in the cluster.
  2. Gravitational lensing
  3. Galaxy clusters shine at X-ray wavelengths as they are filed with hot gases. Scientists use this X-ray data to find the measured properties of the gas so that they infer the mass of the galaxy cluster.
  4. Sunyaev-Zel’dovich Effect: It is the shift in the wavelength of the Cosmic Microwave Background which is the light or electromagnetic radiation left over from the Big Bang. The shift occurs when the light passes through hot gas in the cluster. The size of the shift in the wavelength helps us determine the mass of the galaxy cluster it has passed through.

The Search Continues

Many Organizations are now performing experiments to identify the possible dark matter candidates. Some of the experiments are:

  1. Beneath the Gran Sasso Mountain in Italy, the Laboratori Nazionali del Gran Sasso (LNGS) XENON1T is searching for interactions when WIMPs collide with Xenon atoms.
  2. IceCube Neutrino Observatory, Antarctica has an experiment underneath its ice that is searching for sterile neutrinos. As they only interact with normal matter through gravity
The IceCube Neutrino Observatory is an experiment buried under Antarctica's ice and is hunting for sterile neutrinos which will help us understand dark matter.
The IceCube Neutrino Observatory is an experiment buried under Antarctica’s ice and is hunting for sterile neutrinos which will help us understand dark matter. (Image IceCube Lab)
  1. The European Organization for Nuclear Research (CERN) lab, Switzerland is also searching for dark matter by interacting its candidate particle with antimatter through the Large Hadron Collider (LHC).
The Large Hadron Collider at the CERN lab
The Large Hadron Collider at the CERN lab (Image: CERN)

1...678Page 8 of 8

About us

thehavok.com is a platform where we post original content on Science, Technology, Crypto, Anime, etc. to its readers. We aim to give our reader lucid and simple to read content about recent advancements, concepts, breakthroughs and many other new things from various categories.

Categories

Latest

Fake Paper Publications: Employing Deepfake Technology to Research Reports

News 0
In mid-March, a one-minute video of Ukraine’s president Volodymyr...

One Piece Film Red Anime Reveals Trailer, New Cast Members and More Details

Anime 0
A live stream event for the upcoming One Piece...

The Earth’s Core Moves Far Beneath Our Feet: Findings of Novel Research

News 0
The inner core of the earth oscillates as assumed earlier by the scientists. This article provides further clarifications.

Subscribe

Subscribe to our weekly
Science Sizzlers
Techno Twisters
Crypto Crunchers

© 2021 thehavok | All Rights Reserved