Black holes are highly gravitating objects concentrated at an extremely small region. The study of a black hole is the study of Quantum Physics and General Relativity (Gravity).
Let’s talk about black holes first.
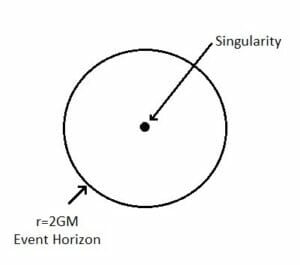
For a black hole of mass M, the radial distance r = 2MG is known as “Event horizon”. It is that distance from which nothing, not even light can escape. If you are inside horizon you are doomed. You will eventually fall into the centre of black hole which is known as “singularity”.
Einstein’s GR talks about gravity in terms of the curvature of space-time. So, let’s see what we can say about black holes in terms of GR we already know.
Suppose there are two people: Alice and Bob. Let’s say Bob jumps into the black hole, sacrificing himself for science, and Alice stays at some distance and watches him. From special relativity, we already know that the time experienced by both of them will be different.
So, let’s see what both of them observe when they are far away from the horizon. As Bob is falling into the black hole, he will not see anything peculiar. But Alice sees that Bob is slowing down as he moves towards the horizon. This is due to gravitational time dilation.
Where t is the time experienced by Alice, and t’ is the time experienced by Bob. We can see that as r decreases, 𝚫t0 increases. If we put r = 2MG, 𝚫t0→ ∞ i.e, Alice will see that it will take infinity time for Bob to reach the horizon. Alice will see Bob slowing down, but never reaching the horizon.
Also, another effect, the length contraction, comes into play, and Alice sees Bob’s length getting shortened as he will move towards the horizon. So what Alice observes is that Bob’s length gets contracted and he is slowing down as he reaches the horizon, but for her, Bob never reaches the horizon, he is squished into an infinitesimally thin layer without even reaching the horizon.
But coming to Bob, he will never experience anything peculiar, and just normally falls into the black hole.
The solution to Einstein’s field equations says that the geometry of space-time near the horizon is smooth. So Bob necessarily does not experience anything weird. But once he is inside the horizon, no matter how hard he tries, he cannot escape falling into the singularity Even if he moves radially outwards, he will follow a spiral path and eventually meet singularity. Gravity there, is so strong, that even light can’t escape out.
Thus it can be said that the event horizon is a point of no return.
One of the best ways to describe all these processes through a diagram is using Kruskal-Coordinates. Getting used to them is a bit difficult but we’ll see.
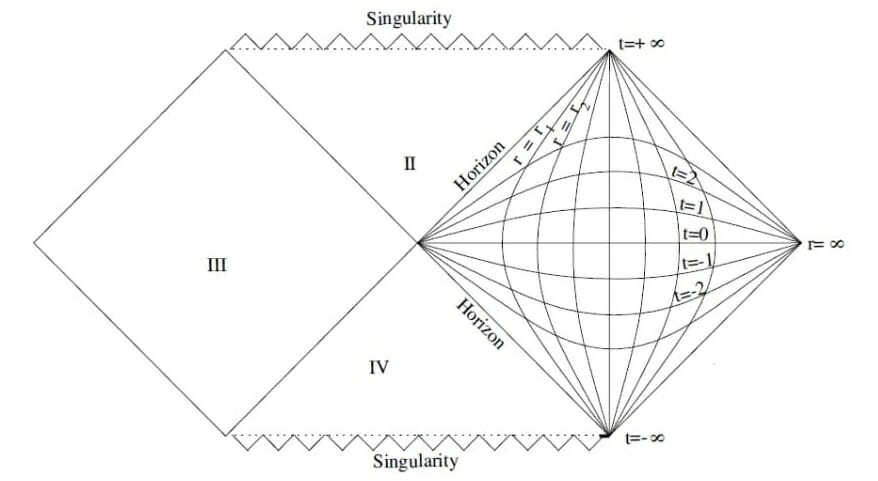
Quadrant I is the exterior of black hole and the big cross at the centre is the horizon. Quadrant II is the interior of the black hole.
If you draw lines at 45 degrees, that will represent the path taken by light and any other massive particle will take a path inside that region.
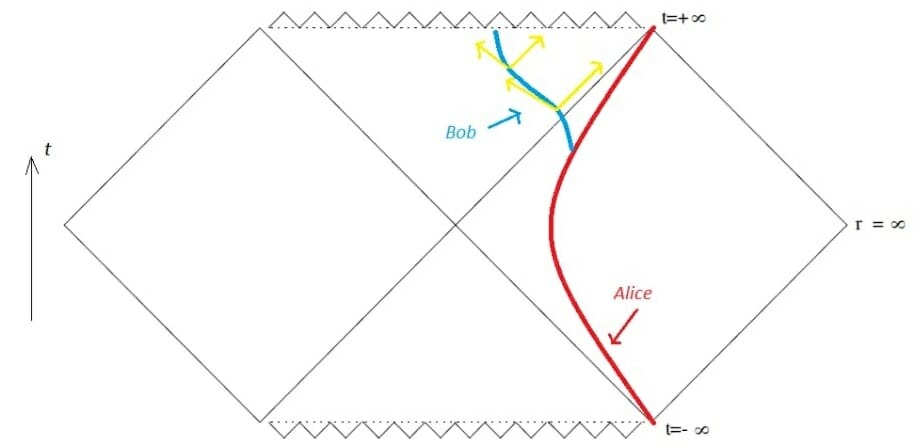
As you can see from the diagram, when you are inside the horizon, you cannot draw any lines which allow you to go back to the Ist Quadrant. The only place where you can go to is the singularity. From the diagram, it looks as if the singularity is not a place but a moment in time because it looks like the time slices t=0,1…etc.
So as we can see from the diagram, Bob will eventually meet the singularity.
Let’s talk about entanglement for a while. Entanglement is the backbone of quantum physics. Let’s take an analogy. Suppose we have 2 pebbles, one red and one blue. We give one to Bob and one to Alice without telling them which one is which and send both of them far away from each other, say 1 light year. Now if Bob looks at his pebble and sees that he has a blue pebble, he instantly knows that Alice has the red one. This sort of correlation is called entanglement.
The point of interest is that the vacuum is entangled. The vacuum we see is not empty. It seems senseless but let us put some sense to it.
Imagine a region of vacuum and divide it into two segments by a partition.
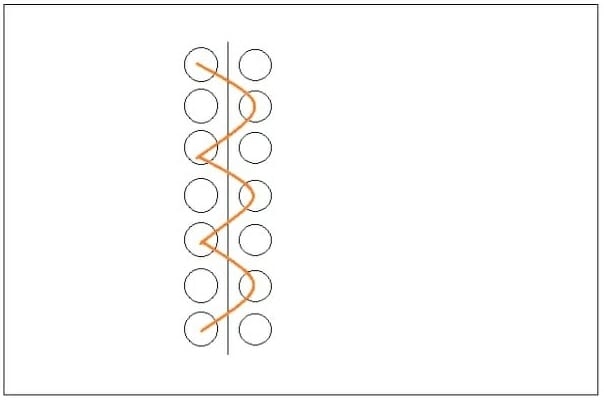
What we mean is, the vacuum is composed of different fields. There might be energy fluctuations inside it causing an electron-positron pair to form. So if we look at a small region on the left side, and we find a particle present, then we will know that there is another particle on the right side, and vice versa. This is because the vacuum is entangled.
Entanglement is what binds the universe together, and is the key to the isotropic nature of the universe.
Now coming back to the Kruskal coordinates, we had left out the Quadrants III and IV. They are part of another black hole which s somehow connected to the first black hole.
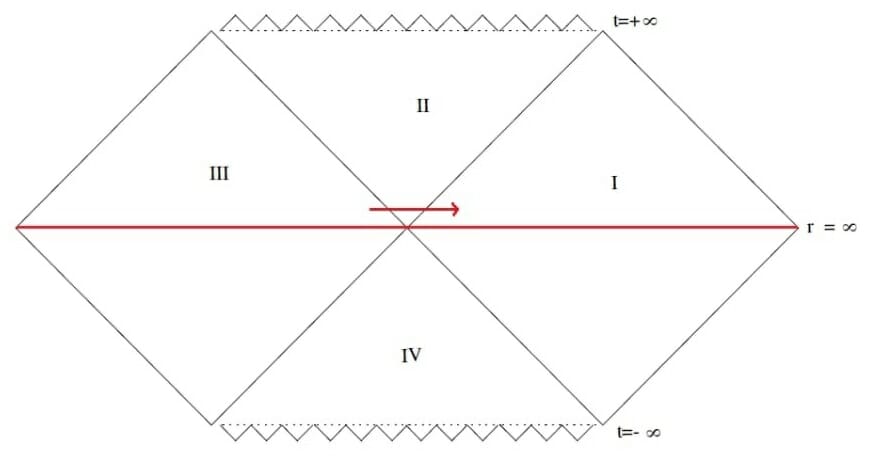
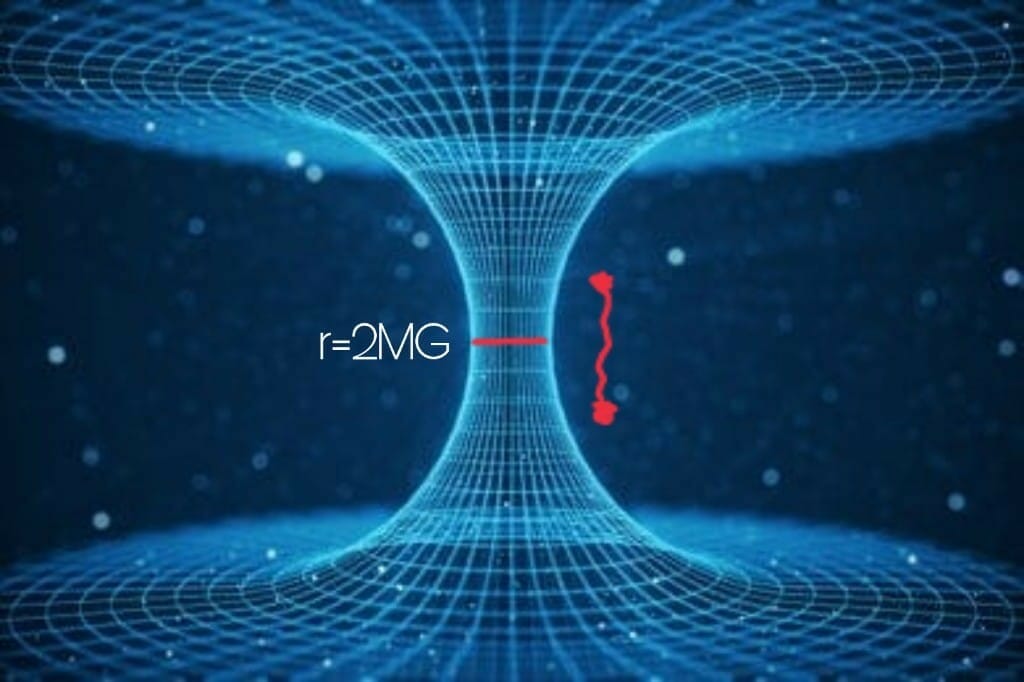
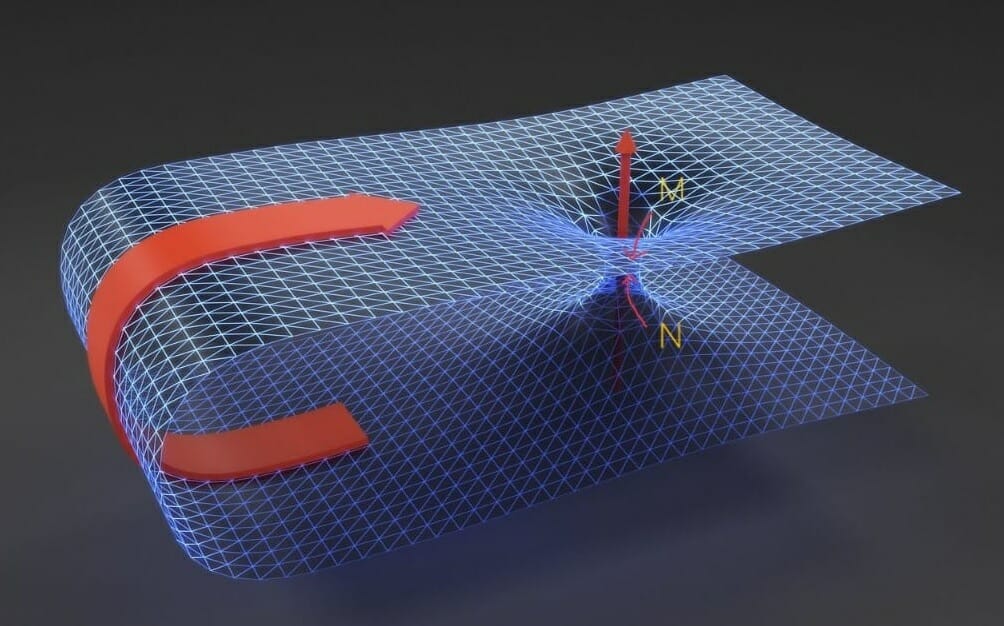
If we somehow manage to move horizontally from Quadrant III to I (do note that physics does not allow this, as this requires moving faster than the speed of light), we’ll move from one black hole to other, even if these are separated by a huge distance in space, i.e. both black holes are connected somehow. And this connection is called a “wormhole” or Einstein-Rosen bridge.
From the Kruskal-coordinates, we see that the geometry is smooth moving from one black hole to another, i.e. nothing is there except space inside the wormhole. But we already know that space is entangled. So now if we take a small region near the event horizon of each black hole, it is entangled.
Strictly speaking, these two black holes are entangled with each other. Entanglement is the thing that connects these two black holes which might be even 1000 light-years apart.
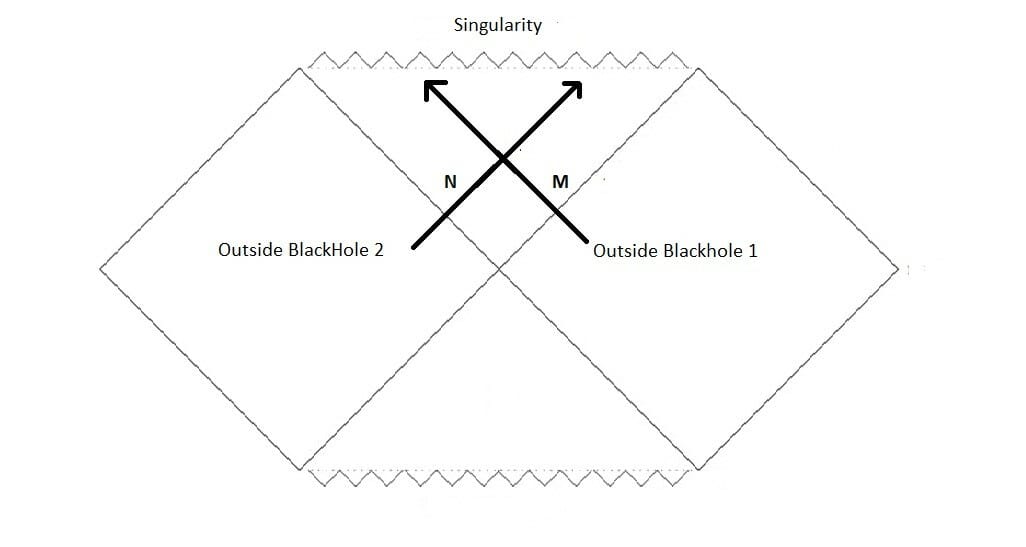
The two black holes are connected to each other by a small region of the event horizon. It looks as if we go inside one, we end up coming out of the other as seen from the diagram. But in reality, once we enter the event horizon, we do not have enough energy to come out of it. The only thing that is possible is, suppose we have two particles, say M and N going inside from each black hole, they both will meet at the entangled region of the horizon.
The same thing can be understood from the Kruskal coordinates.
I.e. they can only meet inside the horizon and they both will meet at the singularity.
Thus, black holes are the topics of utmost importance for both general relativity and quantum physics. There are many paradoxes about black holes, some solved and some yet unsolved.




[…] provides the same to qubits. Entanglement is also necessary for other experiments like this- Blackhole one. Now to work properly, we need states which cannot be described as a product of two single-particle […]
[…] Black holes are the most troublesome creatures in the fascinating zoo of the universe. They are the most despicable objects, throwing up unimaginable infinities and unending paradoxes, making physicists the laughing stock of the world. Unable to resolve these paradoxes or contain these infinities, physicists are stuck in a limbo, where they can neither explain and embrace nor reject and discard the existence of these entities. Yet these remain as the most elegant entities, enclasping the extremum, encoding the infinity, and imagining the incongruity.Last week showed the global recognition of black holes, with the Nobel prize in physics being awarded to people who proved that black holes are an unavoidable prediction of the theory of General Relativity, and also people who discovered the presence of a black hole in the centre of the milky way. But now, out of the blue, what if I tell you that black holes are not really black, but they emit radiation in contrast to their very name… […]
[…] Black holes are a super-dense collection of matter that collapses from a giant star or stars and has a strong field of gravity that nothing can escape its grasps, not even light. Physicists know black holes as a singularity, a point with zero radius and infinite density. The Theory of General Relativity predicts that a sufficiently compact mass will able to deform space-time to form a black hole. The boundary of the region from which no escape is possible is known as the Event Horizon. Even though the event horizon has an impact on the circumstance and fate of an object crossing it, so according to General Relativity it has no locally detectable features. […]
Nice one