The principle of relativity stated that the laws of physics are invariant in frames moving relative to each other with constant velocity. The relation between positions in two frames of reference was given by the Galilean transformations. But when physicists found out that Maxwell’s laws of electromagnetism were not invariant under Galilean transformations, the physics world was in chaos. There were only two possibilities. Either Maxwell’s theory which gave promising results was wrong, or the Galilean transformation was not the right one and it needed a correction.
In 1905, Einstein came up with the special theory of relativity. He inculcated the transformation equations mathematically developed by Lorentz, rather than the Galilean transformation and showed that this was, in fact, consistent with Maxwell’s theory. This theory was a revolution in physics and it changed most of the physics we know today.
Einstein proposed the universe was not the intuitional 3-D space but is actually 4-D. Instead of treating time as a parameter, Einstein treated time as a dimension winded with the other 3 spacial dimensions, making space-time 4 dimensional.
Here we will use the top-down approach rather than the bottom-up approach to get ourselves into the special relativity. We will think of time just like space except for the fact that we can move only forwards in time. Another thing to bear in mind is that no object can go faster than the speed of light, 299,792,458 m/s.
In Newtonian mechanics, we think of the whole of the space at a given instance of time. But this approach is completely flawed. The division of space-time to space and time is not specified by nature but is something made up by us. All the paradoxes regarding the special theory of relativity will disappear if we think about space-time universally. In special relativity, time is not universal, it is different for observers moving relative to each other with different speeds. In 3-Dimensional Euclidean Space, the shortest distance between two points is a straight line. But in a 4-Dimensional space-time, straight line corresponds to the longest interval (we can call this interval the elapsed time), this being the result of the fact that the more you move in space, the less you experience time. More specifically, the rule of thumb is that “on a curly line, you always experience less time”. The formula for obtaining the elapsed time interval is given by
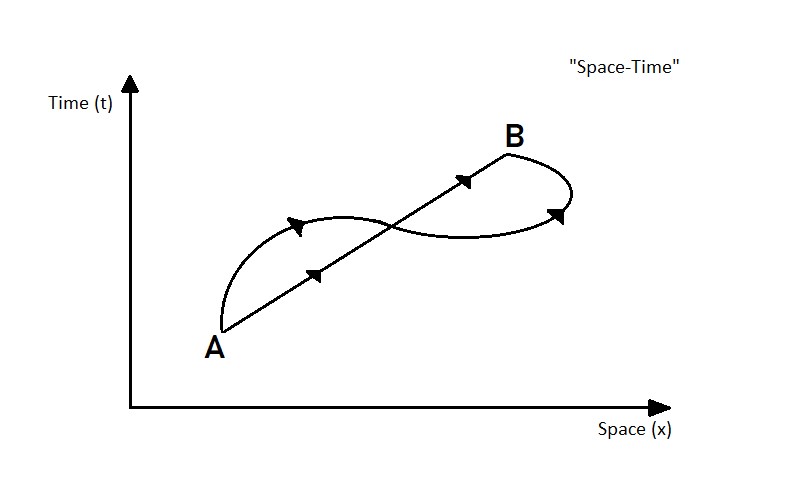
There is a famous paradox (not actually a paradox, so let’s call it a pseudo-paradox) called the twin paradox. Suppose there are twin siblings Alice and Bob. They synchronise their clocks, then Bob sets on a journey to a distant star, say Alpha Centauri, in a rocket with constant velocity and then comes back to Earth. Alice has aged more than Bob. This is because Bob has travelled more distance in space, i.e he has taken the curvier path, while Alice has stayed in the same place.
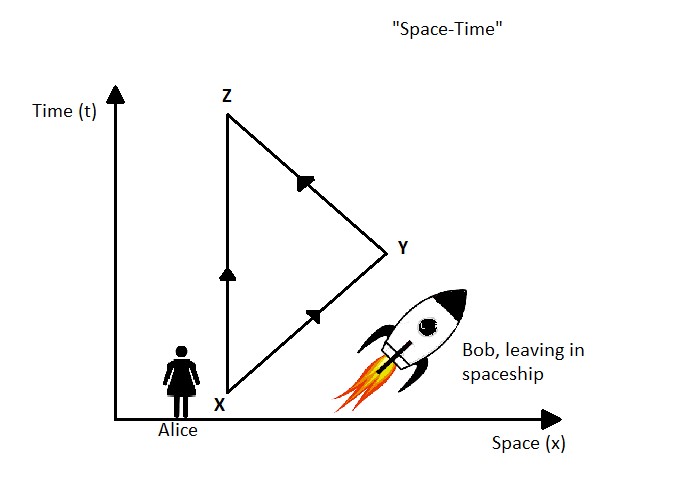
But, from the equivalence principle, there should be no experiment that can show who is stationary and who is moving. Thus for Bob, Alice should be moving and hence she should be aged less than Bob. So is the equivalence principle violated? If we look closely, the principle is not violated, because Bob has to accelerate to return to Earth. So truly speaking, his frame of reference is not inertial.
The paradox says that by the virtue of symmetry, according to the reference frame of Bob, Alice has moved away and come back, so it poses a question as to why Bob has aged lesser than Alice and not vice versa. The reason this happens is that they both travelled different “space-time” distance. So, we have seen that if we talk in terms of space-time, “there are not any actual paradoxes”. It is just because we are not ‘used-to’ with high velocities. We are just not familiar with objects moving with velocities compared to that of light.
So was Newton wrong? No, he was not actually…
For now, consider the speed of light to be 1, thus the distance travelled by light is the same as time elapsed, x = t.
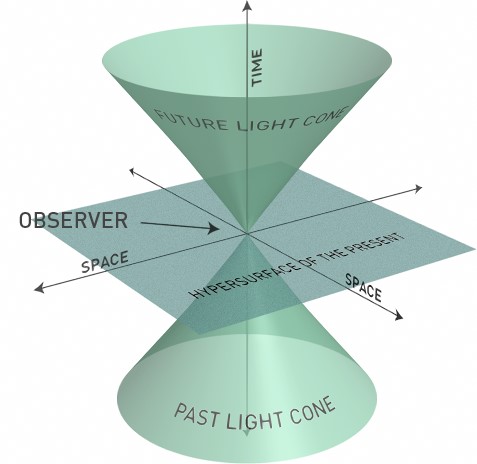
In two dimensions (1 space and 1 time), the path followed by light forms a straight line
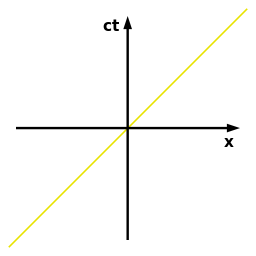
The upper half of this cone is called the future light cone, and the lower half is called the past light cone. Any massive body always moves in a trajectory which is always inside the light cone.
The region outside this cone is called spacelike, no massive particle can reach this region. The region inside the cone is called timelike, with all massive particles taking timelike trajectories. The cone x = t is called “lightlike” or “null” trajectories. This is the path taken by light (photons).
So why hadn’t Newton noticed such a thing? This is because the speed of light is very huge. If we draw the cone in standard units of one meter and one second, it would look like,
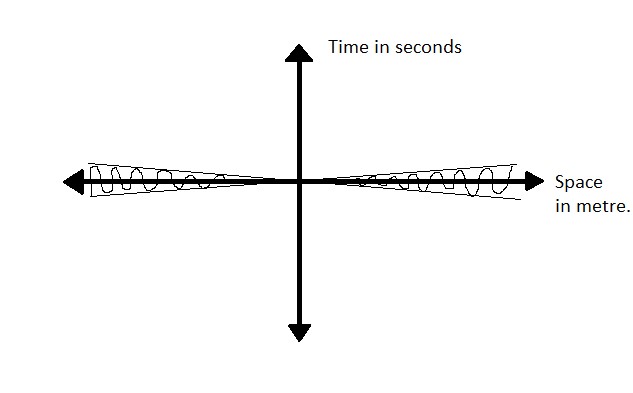
So Newton was not wrong, but he did not consider the finiteness of the speed of light. All of Newtonian mechanics can be obtained as a limit of relativistic mechanics, the limit v<<c.
Einstein did not stop here. He was puzzled by Newton’s gravity and the possibility of sending gravitational signals instantaneously. So he went on further to give the relativistic theory of gravity, the general theory of relativity (GR). In GR, spacetime is not flat but curved, and gravity is nothing but the manifestation of curvature of spacetime.



This paragraph is in fact a fastidious one it assists new internet viewers, who are wishing in favor of blogging.
Keep on writing, great job!
Hi to every one, it’s really a nice for me to pay a quick visit this site, it consists of useful Information.
I go to see every day some web sites and websites to read articles or reviews, but this blog provides feature based content.
Awesome work dude
Keep it up
👍👍
Nice work guys