Major Mathematics Breakthroughs Of 2020

Mathematics is the most fascinating form of science – with its awesome theories and predictions and proofs; it is always fun doing maths. With its wide application in each and every field of research, there is always something new to find in it and discover more in it. Here we present recent breakthroughs in mathematics from 2020 and recent years so far.

Mathematics

Sum of three Cubes problem for the first 100 Numbers have been found.

Our thirst for finding patterns is unquenchable. Mathematicians wondered how can you express the number 33 as the sum of three cubes i.e. . But it went unsolved for 64 YEARS (Yes ! You read it right 64 years !).

The solution is as follows

33^2 = (8866128975287528)^3 + (-2736111468807040)^3 + (-8778405442862239)^3

You can surely try but calculators won’t be able to compute. The numbers are in quadrillion range i.e. 1 followed by 15 zeros.

Mathematics Breakthroughs:
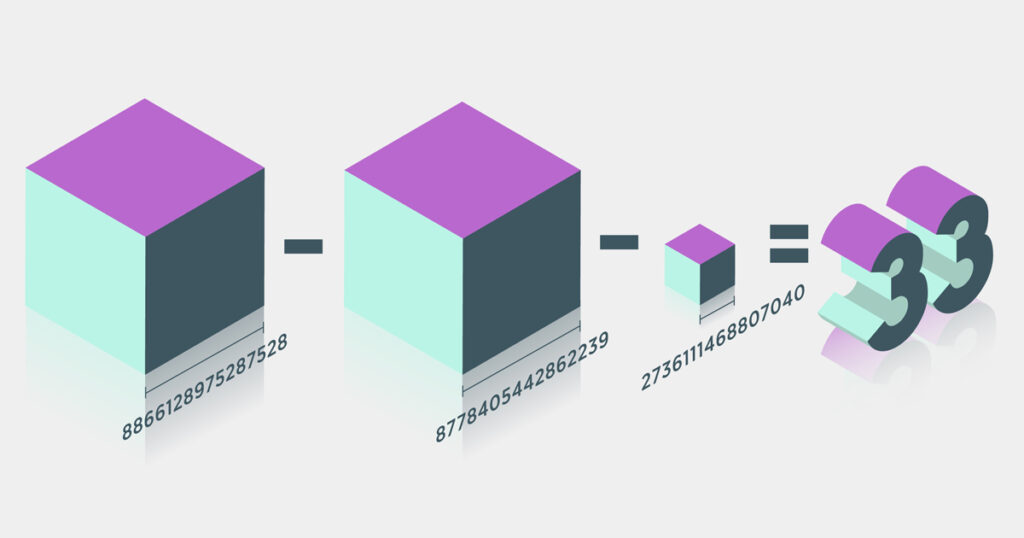
Sum of three Cubes problem
(image: Quanta magazine)

The solution was found by a Mathematician Andrew Booker of the University of Bristol. So how did he come up with the solution? Well, a simple approach would be to try every triplet of (x,y,z) until you came up with a definite answer but even with supercomputer finding a set of (x,y,z) in such large range of numbers is a tedious job.

A better approach would be to write the equation as 33 = x³ + y³ + z³ and we know that sum of two cubes can be factored as . So for a number found in LHS by putting a value in z we try to factor that number n the form this & if it can be factored then we have our solution. But, it is still not easy. With the help of this little trick and number theory Andrew Booker was able to find the solution. The solution itself took 3 weeks of time for a supercomputer because the range in which the solution was found is very large $(10)^{15}$

The equation x³ + y³ + z³ = 2is called Diophantine equation and its solution must have integral values and it becomes more fascinating because there is no mathematical method to tell us whether any given Diophantine equation has solution(s) or not (one more mystery).

The other case like 33 is of number 42 whose solution is found by Andrew Booker and Andrew Sutherland (Mathematician at MIT).

This leaves us to the lowest unsolved case for number 114.

Mathematics

A new way to solve the Quadratic Equations

You must have encountered equations of the form

well the solution is easy Right!

The first method would be apply the Sridhar Acharya’s formula :

$(-b \pm \sqrt {b^2 - 4ac})/2a$

or to guess two numbers such that their sum is B/A and their product is C/A

If you use the first method then you would have to calculate the square root of the term which can be quite mind boggling and if you use the guessing method it does not always work especially when the negatives are involved.

This method was discovered by Professor Po-Shen Loh of Carnegie Mellon University. The method is so simple that it can be integrated into mainstream curriculum in schools and anyone with proper knowledge of Quadratic Equations can discover this method himself (Not Joking!!).

Well we know that,

So if we can solve this method in reverse then we can solve Quadratic Equations easily !!

Let’s try the reverse process for the equation

It would be easier if we could write the above equation in the form $(x -) \times (x -)$ but what to put in those blank spaces? The most common method would be guessing two numbers whose sum is -5 and product is -24. it can be frustrating as it has many possibilities.

We know that sum of roots is -B/A which is 5 and the product of roots is C/A which is -24.

Expressing this in form of variables

α+β = 5

αβ = -24

Here α and β are the roots of the above equation, so if we can express the roots in the form $(a + b) a n d (a - b)$ our job gets a lot easier. The sum of roots is 5 so on taking average of the sum we get 5/2 and try to look for numbers in the form (5/2+k) and (5/2-k) these two numbers automatically add up to 5 so we need them to multiply to -24 which can be done easily…

as seen earlier it is in the form of and can be solved easily upon solving you get

It does not matter if you take the Positive value of k or the Negative value (try yourself).

Indeed 8 and -3 are the two numbers which add up to 5 and whose multiplication is -24 and they also satisfy the equation

Here’s another example

Coefficient of x represents sum of roots which is -1 and its average is -1/2

the numbers add to -1. So on satisfying the other condition (product of roots is -20)

i.e.

with simple algebra you get two values of k which is $\pm 9/2$ and again you can use any value of k

and (let’s go with the positive one!!)

4 and -5 are the roots of the equation and also can be expressed in the form $(x - 4) \times (x + 5)$ (remember sign convention).

So next time you encounter quadratic equation(s) solving them is going to be easy-peasy.

Mathematics

Collatz Conjecture: The Most Fascinating Mathematics

Mathematician Terence Tao showed us that the Collatz conjecture is almost true for almost all numbers. We still do not have full proof of the conjecture but an advancement has been made by professor Tao.

Before jumping into what Collatz conjecture is, remember this “trying to solve this conjecture is like falling into its spell and giving up your useful time”.

Jeffrey Lagarias stated in 2010 that Collatz Conjecture “is an extraordinarily difficult problem, completely out of reach of present-day Mathematics”

Lothar Collatz introduced this idea in 1937, two years after receiving his Doctorate.

The problem is simple and fascinating and you can also explain it to people with no mathematical background. Just pick a number(any); if the number is odd multiply it by 3 and add 1; if the number is even, then divide the number by 2. Now repeat these steps with the new number and repeat again and again. Eventually, you would be stuck in an endless loop or that’s what would happen.

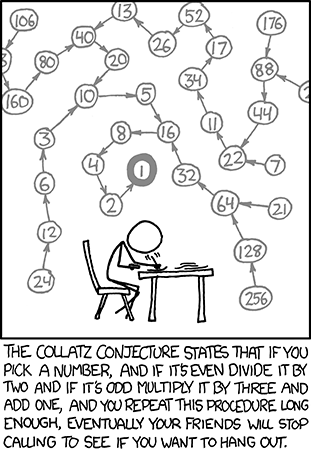
$f(x)=\begin{cases} x/2, \text{if $x$ is even} \\ 3x+1, \text{if $x$ is odd} \end{cases}$

Mathematics Breakthroughs:
Collatz Conjecture
(image: i-programmer)

For example 11: It’s odd, so we triple it and add 1. We have 34, which is even, so we halve it to get 17, triple that and add 1 to get 52, halve that to get 26 and again to get 13, triple that and add 1 to get 40, halve that to get 20, then 10, then 5, triple that and add 1 to get 16, and halve that to get 8, then 4, 2 and 1. And we’ve stuck in the loop again.

So if you start with any positive integer you would always end up in a loop. The most fascinating thing about this conjecture is that it is true for any particular number but it is difficult to prove it for every number.

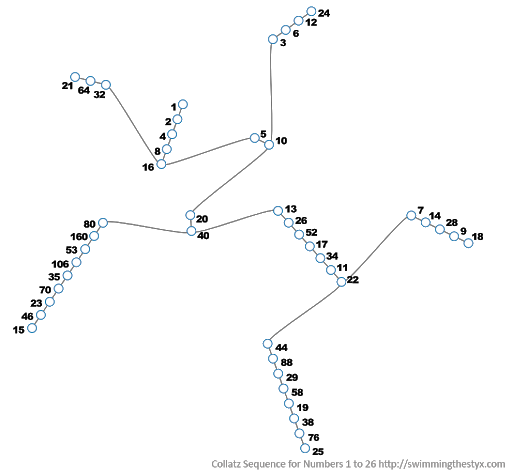
Graphing Some of the Collatz Numbers
(image: Swimming the STYX)

An anonymous reader commented on professor Tao’s blog that instead of solving it completely why not solve for almost all the numbers. Professor Tao was inspired by this comment and made some great progress in proving the Collatz Conjecture. The conjecture continues to attract mathematicians so why not give it a try but remember not to get stuck in its endless loop.

Mathematics

With such breakthroughs mathematics continues to stay fascinating, fun, advanced and progressive all at the same time.

To know About “The Abel Prize” – which is awarded to such breakthroughs of mathematics and encourage betterment of whole mathematics field – Click Here

Mathematics